AT_xmascon23_a Art Irrationnel

请从 $k = 2, 3, 4$ 中选择一个，并回答下述问题。 请用若干个边长比例为 $1 : \left(1 + \sqrt[k]{2}\right)$ 或 $\left(1 + \sqrt[k]{2}\right) : 1$ 的长方形，不留缝隙且不重叠地拼成一个正方形。更详细的限制条件请参见“输出格式”部分。 **[可以在此处使用简易可视化工具。](https://hos.ac/contest/xmas2023/art_irrationnel.html)**

输入为空。

请按如下格式输出： > $k$ $r$ $n$ $a_1$ $b_1$ $c_1$ $d_1$ $a_2$ $b_2$ $c_2$ $d_2$ $\vdots$ $a_n$ $b_n$ $c_n$ $d_n$ - $k$ 是你选择的 $2, 3, 4$ 之一。 - 实数 $r$ 的具体表示格式见下文。它表示你所构造的正方形的顶点为 $(0, 0)$、$(r, 0)$、$(r, r)$、$(0, r)$。 - $n$ 表示长方形的数量，需满足 $1 \le n \le 10^5$。 - 实数 $a_i, b_i, c_i, d_i$（$1 \le i \le n$）的表示格式见下文。表示第 $i$ 个长方形的四个顶点为 $(a_i, c_i), (b_i, c_i), (b_i, d_i), (a_i, d_i)$。 - $r$ 以及每个 $a_i, b_i, c_i, d_i$（$1 \le i \le n$）都需输出 $k$ 个整数 $p_0, p_1, \ldots, p_{k-1}$，空格分隔，表示该值为 $\sum_{j=0}^{k-1} p_j (\sqrt[k]{2})^j$，其中 $-10^9 \le p_j \le 10^9$。 - 必须满足 $r > 0$。 - 对每个 $1 \le i \le n$，需满足 $0 \le a_i < b_i \le r$ 且 $0 \le c_i < d_i \le r$。 - 对每个 $1 \le i \le n$，需有 $\dfrac{d_i-c_i}{b_i-a_i} = 1 + \sqrt[k]{2}$ 或 $\dfrac{b_i-a_i}{d_i-c_i} = 1 + \sqrt[k]{2}$。 - 正方形的所有内部点及边界点必须完全被这 $n$ 个长方形的内部或边界覆盖，且任意两个长方形的内部不得有正面积的交集。

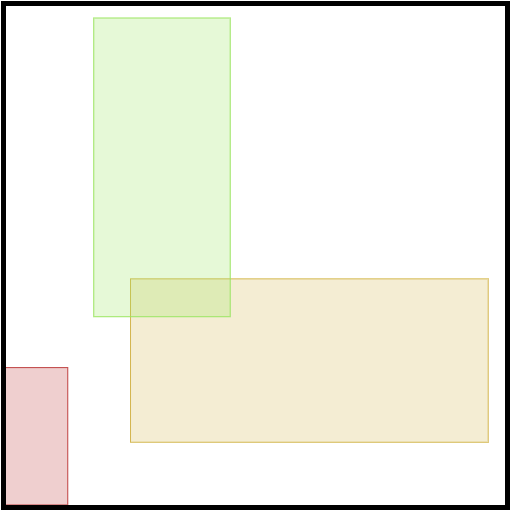### 样例说明 1 此为**除了最后一条条件外**都满足的输出样例（因此会被判定为不正确）。下图展示了此例中长方形的排布（左下角坐标为 $(0, 0)$，右下角为 $(r, 0)$）： 输出示例 **[可以在此处使用简易可视化工具。](https://hos.ac/contest/xmas2023/art_irrationnel.html)** 由 ChatGPT 5 翻译