AT_xmascon24_a Artistic Modulus

对于每个输入文件，将给出 $T$ 个测试用例。对于每个测试用例，给定一个如下所述的图 $G$，请回答以下问题。 $G$ 是一个有 $N$ 个顶点、$M$ 条边的无向简单图。顶点编号为 $1, 2, \ldots, N$。第 $i$ 条边（$1 \le i \le M$）连接顶点 $A_i$ 与 $B_i$。 你需要考虑如下的涂色方法：将 $G$ 的每个顶点和每条边涂成**金色**或**银色**之一（这样的涂色方法共有 $2^{N+M}$ 种）。**艺术性涂色**指满足以下所有条件的涂色方法： - 对于任意**金色**的边，它所连接的两个顶点中至少有一个是**金色**的。 - 对于任意**银色**的顶点，与它相连的边中至少有一条是**银色**的。 请计算艺术性涂色的方案数对 $2$ 取余的结果。

输入的第 $1$ 行给出测试用例的个数 $T$。之后的 $T$ 个测试用例，各自以如下格式给出： > $N$ $M$ > $A_1$ $B_1$ > $A_2$ $B_2$ > $\vdots$ > $A_M$ $B_M$

对于每个测试用例，依次输出一行，表示艺术性涂色的方案数对 $2$ 取余的结果。

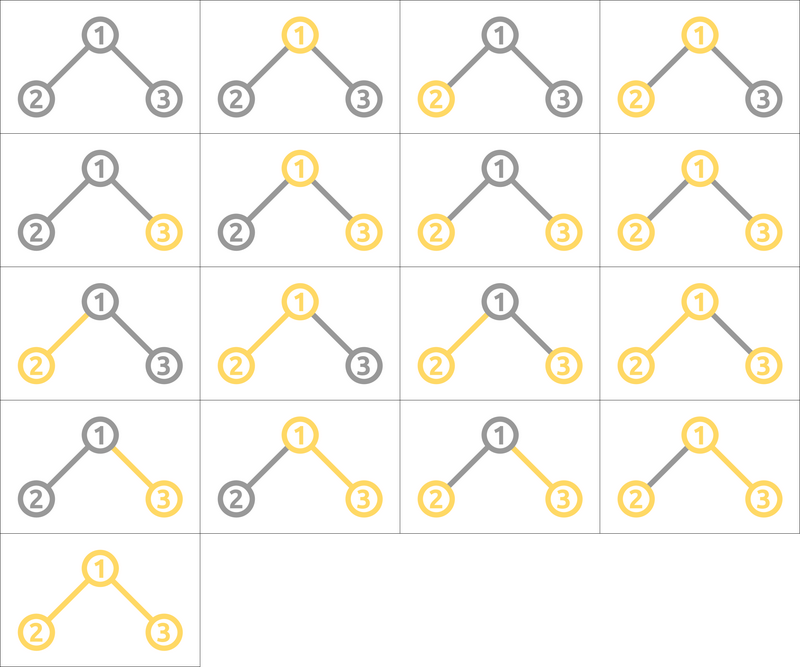
### 示例解释 1 在第 $1$ 个测试用例中，艺术性涂色的方案共有如图所示的 $17$ 种。  ### 数据范围 - $1 \le T \le 100$。 - $0 \le N \le 2024$。 - $0 \le M \le 2024$。 - $1 \le A_i < B_i \le N$ （$1 \le i \le M$）。 - 对任意 $1 \le i < j \le M$，$(A_i, B_i) \ne (A_j, B_j)$。 由 ChatGPT 5 翻译