AT_yahoo_procon2019_final_c Checkered Stamps

有一个 $10^9 \times 10^9$ 的网格。我们用 $(i, j)$ 表示从上往下第 $i$ 行、从左往右第 $j$ 列的格子。每个格子要么是白色，要么是黑色。最开始所有格子都是白色。 现在高桥君要总共盖 $N$ 次印章。第 $i$ 次（$1 \leq i \leq N$），他会用一个高 $H_i$、宽 $W_i$ 的矩形印章，左上角与 $(R_i, C_i)$ 重合地盖在网格上（保证印章不会超出网格范围）。这个印章设计成在全白网格上盖出市松格（棋盘格）图案。具体来说，印章上从上往下第 $p$ 行、从左往右第 $q$ 列（$1 \leq p \leq H_i, 1 \leq q \leq W_i$）的格子，如果 $p+q$ 为偶数，则该格子的颜色反转（白变黑，黑变白），如果 $p+q$ 为奇数，则颜色不变。 请问盖完 $N$ 次印章后，网格上有多少个黑色格子。

输入通过标准输入给出，格式如下： > $N$ > $H_1$ $W_1$ $R_1$ $C_1$ > $\vdots$ > $H_N$ $W_N$ $R_N$ $C_N$

输出盖完 $N$ 次印章后网格上的黑色格子数。

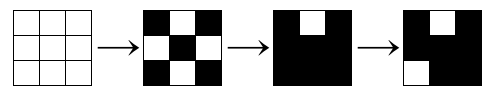
### 限制条件 - $1 \leq N \leq 10^5$ - $1 \leq H_i \leq 10^9$ - $1 \leq W_i \leq 10^9$ - $1 \leq R_i \leq 10^9$ - $1 \leq C_i \leq 10^9$ - $H_i + R_i - 1 \leq 10^9$ - $W_i + C_i - 1 \leq 10^9$ - 所有输入均为整数 ### 样例解释 1 下图展示了左上角 $3 \times 3$ 区域的变化过程。  由 ChatGPT 4.1 翻译