B3974 [语言月赛 202405] 放行李

小 S 推着她的行李箱走上高铁，开启了一段精彩的旅行。 这节车厢的行李架分为左右两列，每一列分别有 $n$ 个位置，从前往后按 $1$ 到 $n$ 依次编号。对于任意两个编号为 $i$ 和 $j$ 的位置（不区分是哪一列），它们之间的距离是 $\vert i - j \vert$。 $\vert x \vert$ 代表 $x$ 的绝对值。当 $x \geq 0$，$\vert x \vert = x$；当 $x < 0$，$\vert x \vert = -x$。 用 $0$ 表示行李架左边一列，用 $1$ 来表示右边一列。小 S 的座位在 $p$ 列的编号 $q$ 的位置处（$p = 0$ 或 $1$，$1 \leq q \leq n$）。 现在小 S 想要在某个位置摆放她的行李箱。然而，已经有一些位置被其它行李占用，所以那些位置是不能摆放行李箱的。小 S 只能选择一个没有行李的空位。 在此基础上，小 S 首先希望行李箱的摆放位置距离她尽可能小。其次，如果有两个**不同列**的空位置和她的位置距离最小且相同，那么小 S 会选择和她在**同一列**的那一个位置。 现在给你左右两列的行李摆放情况，请你找到一个满足条件的最佳行李摆放位置。如果没有任何空位置，请你输出 $-1$。

第一行一个整数 $n$，表示每一列位置数量。 第二行 $n$ 个 $0$ 或 $1$ 的整数，第 $i$ 个整数表示**左列**第 $i$ 个位置是否已经有行李，若为 $1$ 则有行李，若为 $0$ 则没有行李。 第三行 $n$ 个 $0$ 或 $1$ 的整数，第 $i$ 个整数表示**右列**第 $i$ 个位置是否已经有行李，若为 $1$ 则有行李，若为 $0$ 则没有行李。 第四行，两个整数 $p, q$，表示小 S 所在位置是哪一列，在这一列的哪个位置。

输出一行，若有可以摆放行李的位置，则输出两个整数，分别表示最佳位置在左列还是右列，最佳位置与小 S 所在位置的**距离**。 如果没有可以放行李的位置，则输出一个整数 $-1$。

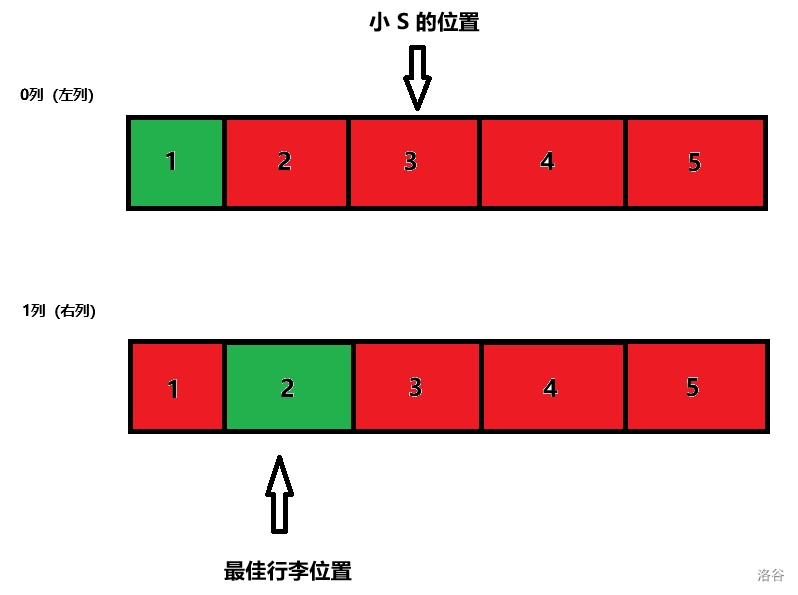
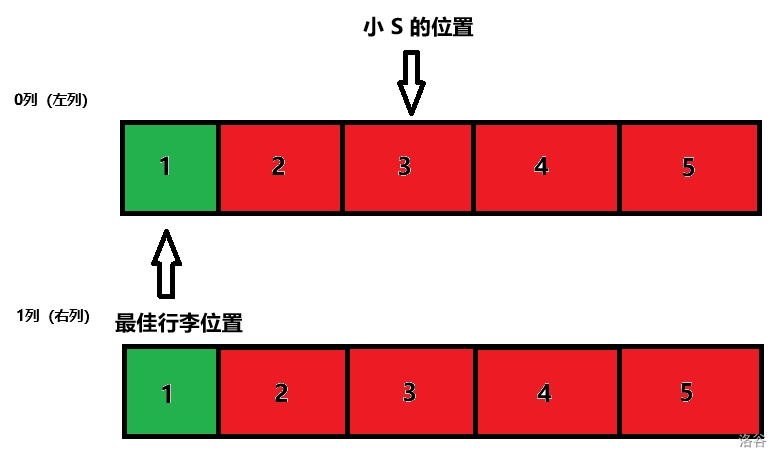
### 样例 1 解释 为了方便观察，我们用$\textcolor{green}{绿色}$来表示没有行李的空位，用$\textcolor{red}{红色}$来表示有行李。 样例 1 如图：  此时由于右列第 $2$ 个位置距离小 S 更近，所以右列第 $2$ 个位置是最佳位置，答案是 `1 1` （表示这个位置在右列，和小 S 位置距离为 $1$）。 ### 样例 2 解释 样例 2 如图：  此时由于两个位置距离小 S 都相同，而左列的那个位置和小 S 在同一列，所以答案是 `0 2` （表示这个位置在左列，和小 S 位置距离为 $2$）。 ### 样例 3 解释 由于没有任何一个空位，所以输出 $-1$。 ### 数据范围 对于前 $30 \%$ 的数据，保证小 S 一定在左列，左列所有位置一定都有行李。 对于另 $30 \%$ 的数据，保证左列有且仅有一个空位置，右列有且仅有一个空位置。 对于 $100 \%$ 的数据，保证 $1 \leq q \leq n \leq 10^6$，$p$ 为 $0$ 或 $1$，第二行、第三行读入的整数为 $0$ 或 $1$。