B4173 [BCSP-X 2024 6 月小学高年级组] 先序遍历

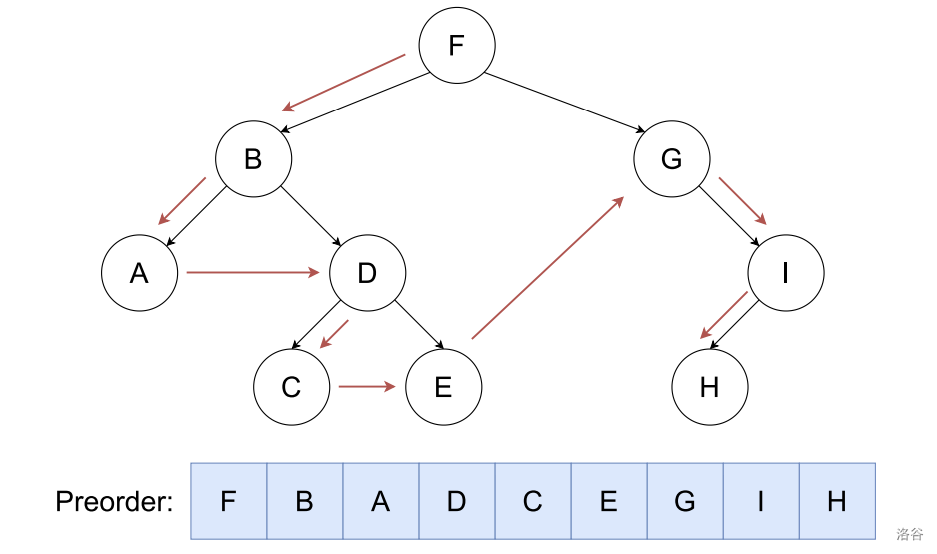
按照根-左-右的顺序遍历**二叉树**： - 先序遍历 = 根 + 左子树先序遍历 + 右子树先序遍历 - 空树的先序遍历 = 空  给一棵 $n$ 个点的二叉树（根节点为 $1$），你可以进行以下操作至多 $1$ 次： - 选择 $1$ 个（除了根之外的）点 $u$，断开 $u$ 和其父节点之间的边；然后重新选择另一个点作为 $u$ 的父节点、将 $u$ 接上去，需要保证操作之后仍然是一棵以 $1$ 为根的二叉树。 你想要操作之后的二叉树有字典序最小的先序遍历序列，输出这个序列。

第一行 $1$ 个整数 $T$，代表有 $T$ 组数据。 每组数据第一行 $1$ 个整数 $n$；接下来 $n$ 行，第 $i$ 行 2 个整数 $ls[i], rs[i]$ 代表 $i$ 号结点的左右儿子编号，没有左右儿子的话用 $0$ 表示。

对于每组数据，输出一行 $n$ 个整数，代表字典序最小的二叉树先序遍历。

### 样例解释 #1 - 对于第一个样例，可以把 3 号结点连在 2 号结点的左儿子处。 - 对于第二个样例，可以把 4 号结点连在 3 号结点的左儿子处。 ### 数据范围 对于所有数据，令 $\sum n$ 代表每组数据中 $n$ 的和，$1 \leq T \leq 100, 1 \leq n \leq 10^5, 1 \leq \sum n \leq 3 \times 10^5$，保证输入是一棵以 1 为根的二叉树。 - 对于测试点 1~3：$n \leq 10$； - 对于测试点 4~8：$n \leq 200$； - 对于测试点 9~11：$n \leq 1000$； - 对于测试点 12~14：$n \leq 10^5$ 且所有 $ls[i] = 0$； - 对于测试点 15：$n \leq 10^5$ 且所有 $rs[i] = 0$； - 对于测试点 16~20：$n \leq 10^5$；