B4322 [科大国创杯小学组 2025] 正方形划分
题目背景
Subtask 0 为民间数据,Subtask 1 为官方数据。
题目描述
小可可发明了一种新的正方形划分方法。
首先我们有一个正方形,我们称该图形为第 $0$ 轮的图形。我们将这个正方形均匀划分成 $4$ 个部分——左上、右上、左下和右下,分别将其编号为 $\tt{ABCD}$,称新的图形为第 $1$ 轮的图形。
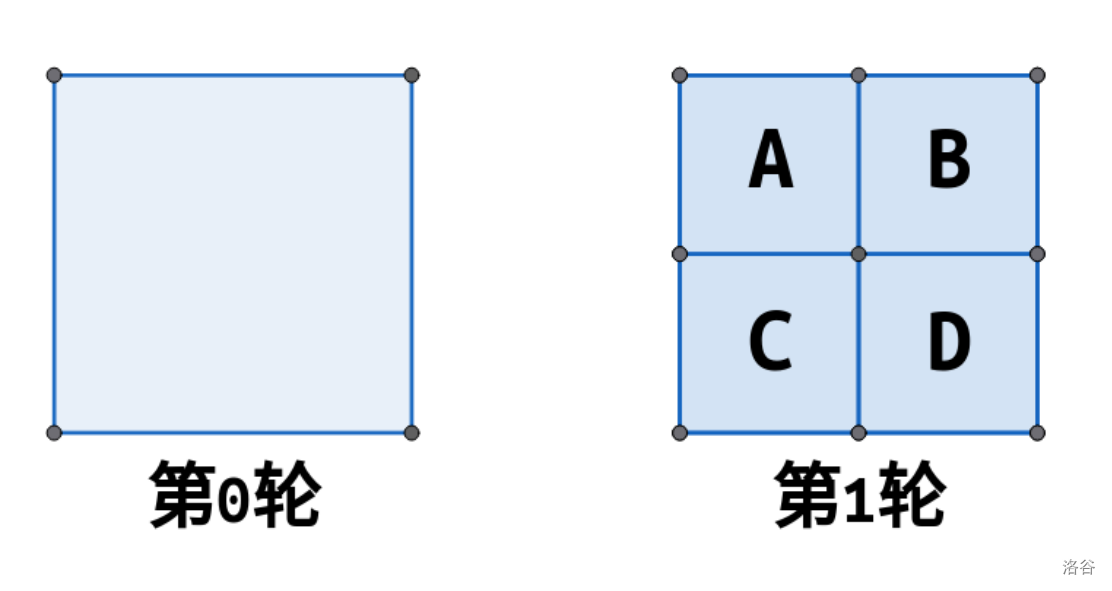
我们再将第一个图形所划分的每一个部分 $\tt{ABCD}$,分别再分成 $4$ 个部分,称新的图形为第 $2$ 轮的图形。对于该图形的每个部分的命名方式为该部分所属第 $1$ 轮的部分的编号 $+ \tt{ABCD}$。如:原来第 $1$ 轮的 $\tt A$ 部分的右上部分的编号为 $\tt{AB}$。
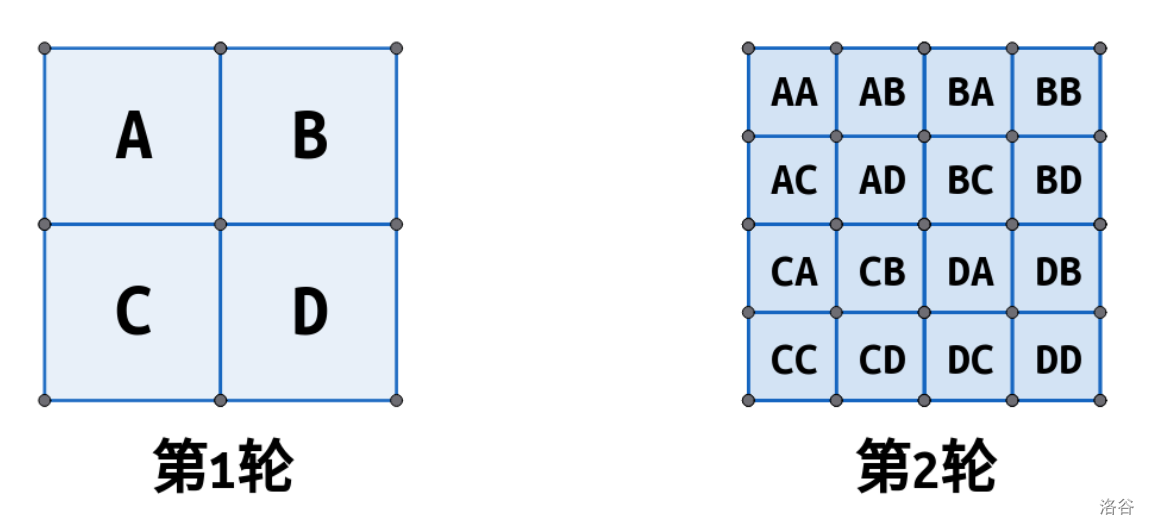
第 $3$ 轮及以上的图形以此类推。这样每个方格都有一个编号,同时也有一个位置,即第几行(从上往下数)第几列
(从左往右数)。现在小可可想实现编号与其位置的相互转化,请你写一份程序帮帮他。
输入格式
本题有多组测试数据,输入第一行一个整数 $T$ 表示测试数据组数,接下来输入每组数据。
对于每组测试数据共一行,有以下两种可能:
- $0$ $n$ $x$ $y$ 表示该测试数据需要求出第 $n$ 轮的图形中第 $x$ 行第 $y$ 列的格子的编号。
- $1$ $str$ 表示该测试数据需要求出编号为 $str$ 的格子的位置。
如果仍然对输入方式不够清楚,可以去观察输入输出样例和样例解释。
输出格式
对于每组测试数据:
- 如果输入的测试数据为 $0$ $n$ $x$ $y$ 的形式,输出一行一个字符串 $str$ 表示该格子编号。
- 如果输入的测试数据为 $1$ $str$ 的形式,输出一行三个整数 $n, x, y$ 表示该格子位于第 $n$ 轮图形的第 $x$ 行第 $y$ 列。
说明/提示
### 样例解释
第一行一个整数 $3$ 表示我们一共有三组测试数据。
第一组测试数据 $0 \ 1 \ 2 \ 1$,表示我们要将第 $1$ 轮图形的第 $2$ 行第 $1$ 列的位置转化为编号,根据题意描述中的图可知编号为 $\tt{C}$。
第二组测试数据 $1 \ \tt{AB}$,表示我们要求出编号为 $\tt{AB}$ 的格子的位置,根据题意描述中的图可知它在第 $2$ 轮第 $1$ 行第 $2$ 列。
第三组测试数据 $0 \ 2 \ 3 \ 4$,表示我们要将第 $2$ 轮图形的第 $3$ 行第 $4$ 列的位置转化为编号,根据题意描述中的图可知编号为 $\tt{DB}$。
### 约定和数据范围
- 数据点 $1$,$1 \leq T \leq 10$,$1 \leq n \leq 2$。
- 数据点 $2, 3$,$1 \leq T \leq 10$,$1 \leq n \leq 10$。
- 数据点 $4, 5$,$1 \leq T \leq 5 \times 10^4$,$n = 10$,即保证所有图形均为第 $10$ 轮图形。
- 数据点 $6$,$1 \leq T \leq 5 \times 10^4$,$1 \leq n \leq 30$,询问仅形如 $0$ $n$ $x$ $y$。
- 数据点 7,$1 \leq T \leq 5 \times 10^4$,$1 \leq n \leq 30$,询问仅形如 $1$ $str$。
- 数据点 $8 \sim 10$,$1 \leq T \leq 5 \times 10^4$,$1 \leq n \leq 30$。