B4469 回形座位 / seat

班主任老师在给你的班级排座位。每个教室可以看作是一个 $N\times N$ 的座位矩阵，每个座位用 $0$ 或 $1$ 表示：$0$ 代表男生，$1$ 代表女生。 现在有同学按照以下规则，记录了这个教室的座位信息： 1. 扫描方式：从矩阵左上角（第一行第一列）开始，按“回”字形顺序遍历整个矩阵——先从左到右遍历第一行，再从上到下遍历最后一列剩余部分，接着从右到左遍历最后一行剩余部分，然后从下到上遍历第一列剩余部分；完成最外层后，继续按相同规则遍历内层矩阵，直至所有座位遍历完毕。 2. 记录规则：用一系列数字交替表示连续的男生人数和女生人数，第一个数字一定代表男生人数（例如：$2,3,1,3$ 表示按顺序先后出现 $2$ 个男生，$3$ 个女生，$1$ 个男生，$3$ 个女生）。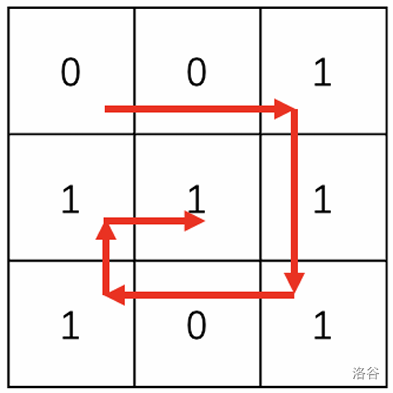 例如： 在长度为 $4$，$3\times3$ 的座位矩阵中，男女生记录序列为：$2,3,1,3$，座位最终的入座顺序和结果为：  现在给定这个记录序列，请你还原出原始的 $N\times N$ 座位矩阵。 数据保证：记录序列中所有数字之和等于 $N\times N$，且序列严格交替对应男生和女生的连续人数。

第一行包含两个整数 $K$ 和 $N$，表示记录序列的长度，矩阵的行数和列数。 第二行包含 $K$ 个正整数，用空格分隔，表示男女生记录序列。

输出 $N$ 行，每行 $N$ 个整数（$0$ 或 $1$），表示还原后的座位矩阵，数字之间用空格分隔。

#### 【样例 $1$ 解释】 - 遍历顺序：$(1,1)\rightarrow(1,2)\rightarrow(1,3)\rightarrow(2,3)\rightarrow(3,3)\rightarrow(3,2)\rightarrow(3,1)\rightarrow(2,1)\rightarrow(2,2)$ - 记录序列解析： 1. 第一个数字 $3$：连续 $3$ 个男生（对应遍历前 $3$ 个位置：$(1,1)$、$(1,2)$、$(1,3)$）； 2. 第二个数字 $3$：连续 $3$ 个女生（对应接下来 $3$ 个位置：$(2,3)$、$(3,3)$、$(3,2)$）； 3. 第三个数字 $3$：连续 $3$ 个男生（对应最后 $3$ 个位置：$(3,1)$、$(2,1)$、$(2,2)$）。 #### 【数据范围】 对于 $10\%$ 的数据，保证 $N=1$； 对于另外 $10\%$ 的数据，保证 $N=2$； 对于另外 $10\%$ 的数据，保证男女生记录序列只包含男生。 对于另外 $10\%$ 的数据，保证 $K=2$。 对于另外 $20\%$ 的数据，保证 $K=N\times N$ 且男女生记录序列都为 $1$。 对于 $100\%$ 的数据，保证 $1\le n\le100,1\le K\le N\times N$，男女生记录序列之和为 $N\times N$。