CF1004D Sonya and Matrix

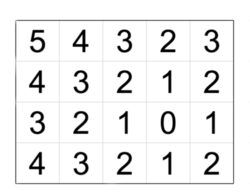
由于 Sonya 刚刚学习了矩阵的基础知识，她决定稍微玩一下矩阵。 Sonya 想象出了一种新型的矩阵，她称之为菱形矩阵。这种矩阵中恰好有一个格子的值为 $0$，而其他所有格子的值都是它们到该 $0$ 所在格子的曼哈顿距离。所有值相同的格子会形成一个菱形，这也是 Sonya 给这种矩阵命名的原因。 两个格子 $(x_1, y_1)$ 和 $(x_2, y_2)$ 之间的曼哈顿距离定义为 $|x_1 - x_2| + |y_1 - y_2|$。例如，格子 $(5, 2)$ 和 $(7, 1)$ 之间的曼哈顿距离为 $|5-7|+|2-1|=3$。  菱形矩阵示例。注意，菱形矩阵由 $n$、$m$ 以及 $0$ 所在格子的坐标唯一确定。 她画了一个 $n\times m$ 的菱形矩阵。她认为，如果只给你这个矩阵中所有元素的一个无序序列（即 $n\cdot m$ 个数的序列），你无法还原出这个矩阵。注意，Sonya 不会告诉你 $n$ 和 $m$，你只能得到矩阵中所有数的一个序列。 请编写程序，找出一个 $n\times m$ 的菱形矩阵，使得其元素与给定序列中的元素相同（顺序可以不同）。

第一行包含一个整数 $t$（$1\leq t\leq 10^6$），表示矩阵中的格子数。 第二行包含 $t$ 个整数 $a_1, a_2, \ldots, a_t$（$0\leq a_i< t$），表示矩阵中所有格子的值，顺序任意。

第一行输出两个正整数 $n$ 和 $m$（$n\times m = t$），表示矩阵的大小。 第二行输出两个整数 $x$ 和 $y$（$1\leq x\leq n$，$1\leq y\leq m$），表示 $0$ 所在格子的行号和列号。 如果有多个答案，输出任意一个即可。如果无解，输出一个整数 $-1$。

你可以在题面中的示例图中看到第一个样例的解。你也可以选择 $(2, 2)$ 作为 $0$ 所在格子。你还可以选择一个 $5\times 4$ 的矩阵，$0$ 在 $(4, 2)$。 在第二个样例中，有一个 $3\times 6$ 的矩阵，$0$ 在 $(2, 3)$。 在第三个样例中，无解。 由 ChatGPT 4.1 翻译