CF1006E Military Problem

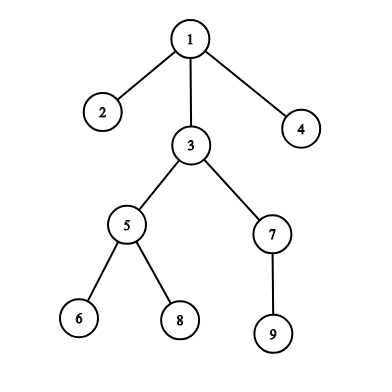
你需要帮助伯兰军队设计命令传递系统！ 伯兰军队中一共有 $n$ 个军官。第一个官员是军队统帅他没有上级。其他每位军官都有且仅有一名直属上级。如果一个军官 $a$ 是军官 $b$ 的直属上级，那么你也可以说军官 $b$ 就是军官 $a$ 的直属下属。 如果满足下列条件，那么军官 $x$ 就是军官 $y$ 的下属（直接或非直接）： 1. $y$ 是 $x$ 的直属上级。 2. $x$ 的直属上级是 $y$ 的下属。 举个例子，下图的官员 $3$ 的下属有: $5,6,7,8,9$。  所以，在伯兰军队的结构中，除了统帅，其他人都是统帅的下属。 伯兰军队可以看作一棵拥有 $n$ 个节点的树，节点 $u$ 就代表了军官 $u$。根（即节点 $1$）就相当于军队统帅。 兰战争部要求你处理 $q$ 个查询，第 $i$ 个查询格式为 $(u_i, k_i)$，其中 $u_i$ 是某位军官，$k_i$ 是一个正整数。 处理第 $i$ 个查询时，需要模拟命令从 $u_i$ 号军官向其下属传播的过程。这里采用典型的深度优先搜索（即 DFS）算法。 假设当前 $a$ 号军官正在传播命令。他会选择一位 $b$ 号直属下属（即节点 $a$ 的儿子节点），要求满足这位直属下属还没有接收过此命令。若存在多个可选下属，则选择编号最小者。随后，$a$ 号军官将命令传递给 $b$ 号军官。之后，$b$ 号军官会以相同算法向其子树传播命令。当 $b$ 号军官完成传播后，$a$ 号军官会继续选择下一个直属下属（采用相同策略）。当 $a$ 号军官无法选择任何未接收命令的下属时，命令传播终止。 同样的，回到上面那张图：  如果军官 $1$ 下达了命令，军官们收到命令的顺序是： $[1,2,3,5,6,8,7,9,4]$ 。 如果军官 $3$ 下达了命令，军官们收到命令的顺序是： $[3,5,6,8,7,9]$。 如果军官 $7$ 下达了命令，军官们收到命令的顺序是：$[7,9]$。 如果军官 $9$ 下达了命令，军官们收到命令的顺序是： $[9]$ 。 这 $q$ 个查询互不干扰。换句话说，这 $q$ 次查询下达的都是不同的命令，相互之间不会有任何影响。

第一行包括两个整数 $n,q$，表示有 $n$ 个军官和 $q$ 个查询 （$2 \le n \le 2 \times 10^5,1 \le q \le 2 \times 10^5$） 。 第二行包括 $n-1$ 个整数 $p_{2},p_{3}\dots p_{n}$（$1\le p_i < i$），表示编号为 $i$ 的军官的直属上级为 $p_{i}$。编号为 $1$ 的军官，即军队统帅，他没有上级，因此不会输入。 接下来 $q$ 行，每行包含两个整数 $u_{i},k_{i}$（$1 \le u_{i},k_{i} \le n$）。其中 $u_{i}$ 表示开始下达命令的军官，$k_{i}$ 表示要输出的军官编号是第几个得知命令的。

一共 $q$ 行，每行包含一个整数表示第 $i$ 个查询的答案：编号为 $u_{i}$ 的军官下达命令后，第 $k_{i}$ 个得知此命令的军官编号是多少，如果传达人数不足 $k_{i}$ 个，请输出 $-1$。

Translate by @[Moya_Rao](https://www.luogu.com.cn/user/814130)