CF1007E Mini Metro

在一个简化版的“Mini Metro”游戏中，只有一条地铁线路，所有列车都朝同一个方向行驶。线路上有 $n$ 个车站，游戏开始时，第 $i$ 个车站有 $a_i$ 个人在等车。游戏从第 $0$ 小时开始。每小时结束时（就在小时结束前几分钟），第 $i$ 个车站会瞬间增加 $b_i$ 个人。如果某一时刻，第 $i$ 个车站的人数超过 $c_i$，你就输了。 玩家有若干列火车，可以安排它们在某些小时出发。每列火车的容量为 $k$ 人。在被安排的小时中间，火车会从第 $1$ 个车站开到第 $n$ 个车站，在每个车站尽可能多地接走乘客，直到达到容量上限。如果前一个车站还有人，火车不能在当前车站接人。 如果同一小时安排了多列火车，它们的容量会合并，并一起运行。 玩家希望能坚持 $t$ 小时不输。请你计算，为了做到这一点，最少需要安排多少列火车。

第一行包含三个整数 $n$、$t$ 和 $k$（$1 \leq n, t \leq 200, 1 \leq k \leq 10^9$），分别表示车站数量、需要坚持的小时数和每列火车的容量。 接下来的 $n$ 行，每行包含三个整数 $a_i$、$b_i$ 和 $c_i$（$0 \leq a_i, b_i \leq c_i \leq 10^9$），分别表示第 $i$ 个车站初始人数、每小时结束时到达的人数和该车站允许的最大人数。

输出一个整数，表示最少需要安排的火车数量。

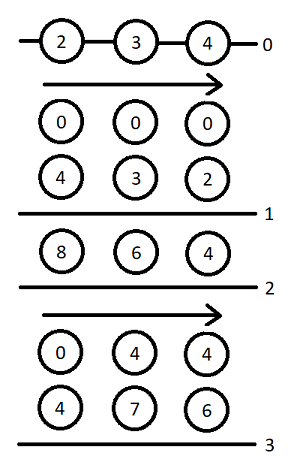
 我们来看样例。共有三个车站，初始时第一个车站有 2 个人，第二个有 3 个人，第三个有 4 个人。各车站的最大容量分别为 10、9 和 8。 一种可行的策略是在第 1 小时和第 3 小时各安排两列火车。这样在第 1 小时，火车会把所有车站的人都接走，小时结束时，第一个车站又来了 4 个人，第二个来了 3 个人，第三个来了 2 个人。 第 2 小时不安排火车，小时结束时，同样数量的人再次到达。 第 3 小时，火车先在第一个车站接走 8 个人，到第二个车站时只能再接 2 个人，因为最多只能带 10 个人。然后火车经过第三个车站时已经满员，无法再接人。之后，车站又分别有新的人到达，游戏结束。 在整个过程中，没有任何车站的人数超过最大容量，因此我们用两列火车赢得了游戏。 由 ChatGPT 4.1 翻译