CF1010F Tree

主火星树生长在火星上。它是一棵二叉树（有根树，每个节点最多有两个儿子），共有 $n$ 个节点，根节点编号为 $1$。它的果实被称为主火星果。现在是夏天，这棵树还没有任何果实。 秋天即将来临，树上的叶子和枝条会开始脱落。显然，如果某个节点从树上脱落，那么它的整个子树也会脱落。此外，根节点会一直保留在树上。形式化地说：树上会保留一个包含根节点的连通节点子集。 之后，果实会在树上生长（仅在保留的节点上）。根节点上恰好会长出 $x$ 个果实。对于每个保留的节点，其果实数不少于其所有保留儿子的果实数之和。允许某些节点上没有果实。 娜塔莎想知道，经过上述变化后，树可能有多少种不同的配置。由于这个数可能非常大，请输出其对 $998244353$ 取模的结果。 如果满足以下任一条件，则认为两种配置不同： - 它们保留的节点子集不同； - 它们保留的节点子集相同，但存在某个节点，其果实数不同。

第一行包含两个整数 $n$ 和 $x$（$1 \le n \le 10^5$，$0 \le x \le 10^{18}$）——树的节点数和根节点的果实数。 接下来的 $n-1$ 行中，第 $i$ 行包含两个整数 $a_i$ 和 $b_i$（$1 \le a_i, b_i \le n$），表示树中的一条边，连接节点 $a_i$ 和 $b_i$。 保证输入数据描述的是一棵以 $1$ 为根的合法二叉树。

输出一个整数，表示可能的树的配置数，对 $998244353$ 取模。

考虑第一个样例。 节点 $1$ 上有 $2$ 个果实。共有 $13$ 种可能的情况： - 节点 $2$ 不存在，节点 $3$ 不存在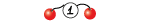； - 节点 $2$ 不存在，节点 $3$ 上没有果实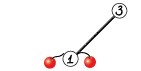； - 节点 $2$ 不存在，节点 $3$ 上有 $1$ 个果实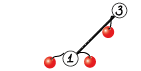； - 节点 $2$ 不存在，节点 $3$ 上有 $2$ 个果实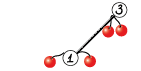； - 节点 $2$ 上没有果实，节点 $3$ 不存在； - 节点 $2$ 上没有果实，节点 $3$ 上没有果实； - 节点 $2$ 上没有果实，节点 $3$ 上有 $1$ 个果实； - 节点 $2$ 上没有果实，节点 $3$ 上有 $2$ 个果实； - 节点 $2$ 上有 $1$ 个果实，节点 $3$ 不存在； - 节点 $2$ 上有 $1$ 个果实，节点 $3$ 上没有果实； - 节点 $2$ 上有 $1$ 个果实，节点 $3$ 上有 $1$ 个果实； - 节点 $2$ 上有 $2$ 个果实，节点 $3$ 不存在； - 节点 $2$ 上有 $2$ 个果实，节点 $3$ 上没有果实。 再看第二个样例。节点 $1$ 上有 $5$ 个果实。共有 $7$ 种可能的情况： - 节点 $2$ 不存在； - 节点 $2$ 上没有果实； - 节点 $2$ 上有 $1$ 个果实； - 节点 $2$ 上有 $2$ 个果实； - 节点 $2$ 上有 $3$ 个果实； - 节点 $2$ 上有 $4$ 个果实； - 节点 $2$ 上有 $5$ 个果实。 由 ChatGPT 4.1 翻译