CF1012B Chemical table

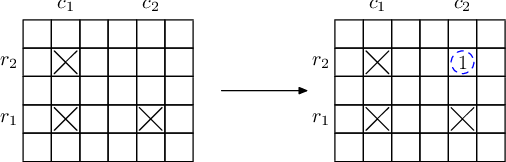
伊诺波利斯大学的科学家们正在继续研究元素周期表。已知有 $n·m$ 种元素，它们组成了一个周期表：一个有 $n$ 行 $m$ 列的矩形。每个元素可以用其在表中的坐标 $(r,c)$（$1 \leq r \leq n$，$1 \leq c \leq m$）来描述。 最近，科学家们发现，对于周期表中任意四个不同的元素，如果它们恰好形成一个边平行于表格边界的矩形，并且他们已经拥有其中三个元素的样本，那么就可以通过核聚变制造出第四个元素的样本。也就是说，如果我们拥有 $(r_{1},c_{1})$、$(r_{1},c_{2})$、$(r_{2},c_{1})$ 这三个位置的元素（其中 $r_{1} \neq r_{2}$ 且 $c_{1} \neq c_{2}$），那么就可以制造出 $(r_{2},c_{2})$ 位置的元素。  用于核聚变的样本不会被消耗，可以在后续的核聚变中继续使用。新制造出来的元素也可以用于后续的核聚变。 科学家们已经拥有了 $q$ 个元素的样本。他们希望最终获得所有 $n·m$ 个元素的样本。为此，他们可以从其他实验室购买一些样本，然后通过任意次数、任意顺序的核聚变制造出剩余的元素。请帮助他们计算，最少需要购买多少个元素的样本。

第一行包含三个整数 $n$、$m$、$q$（$1 \leq n, m \leq 200000$；$0 \leq q \leq \min(n·m, 200000)$），分别表示化学表的行数、列数和科学家们已经拥有的元素样本数量。 接下来的 $q$ 行，每行包含两个整数 $r_{i}$、$c_{i}$（$1 \leq r_{i} \leq n$，$1 \leq c_{i} \leq m$），表示科学家们已经拥有的元素样本的位置。输入中所有元素均不重复。

输出一个整数，表示最少需要购买的元素样本数量。

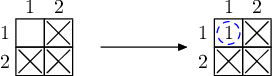
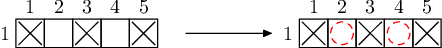
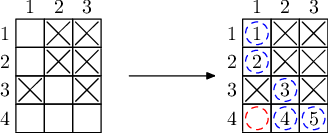
每个样例都配有一张图片进行说明。 每个样例的第一张图片描述了初始拥有的元素样本。黑色叉号表示实验室最初拥有的元素。 第二张图片描述了剩余样本的获得方式。红色虚线圆圈表示需要从其他实验室购买的元素（最优解应最小化红圈数量）。蓝色虚线圆圈表示可以通过核聚变制造出的元素。数字表示制造顺序。 测试样例 1 我们可以利用核聚变，通过已有的三个样本获得第四个元素，因此无需购买任何元素。  测试样例 2 由于只有一行，无法进行任何核聚变，因此必须购买所有缺失的元素。  测试样例 3 有多种可行解，其中一种如下图所示。 注意，在购买了一个红圈元素后，仍然无法立即制造出底行中间的元素（标记为 4）。因此，首先制造左上角的元素（标记为 1），然后在后续核聚变中使用它。  由 ChatGPT 4.1 翻译