CF1016E Rest In The Shades

There is a light source on the plane. This source is so small that it can be represented as point. The light source is moving from point $ (a, s_y) $ to the $ (b, s_y) $ $ (s_y < 0) $ with speed equal to $ 1 $ unit per second. The trajectory of this light source is a straight segment connecting these two points. There is also a fence on $ OX $ axis represented as $ n $ segments $ (l_i, r_i) $ (so the actual coordinates of endpoints of each segment are $ (l_i, 0) $ and $ (r_i, 0) $ ). The point $ (x, y) $ is in the shade if segment connecting $ (x,y) $ and the current position of the light source intersects or touches with any segment of the fence. 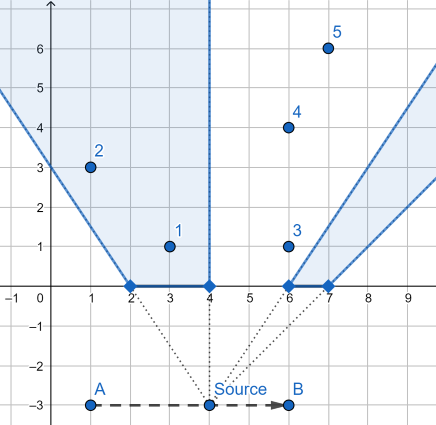You are given $ q $ points. For each point calculate total time of this point being in the shade, while the light source is moving from $ (a, s_y) $ to the $ (b, s_y) $ .

First line contains three space separated integers $ s_y $ , $ a $ and $ b $ ( $ -10^9 \le s_y < 0 $ , $ 1 \le a < b \le 10^9 $ ) — corresponding coordinates of the light source. Second line contains single integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — number of segments in the fence. Next $ n $ lines contain two integers per line: $ l_i $ and $ r_i $ ( $ 1 \le l_i < r_i \le 10^9 $ , $ r_{i - 1} < l_i $ ) — segments in the fence in increasing order. Segments don't intersect or touch each other. Next line contains single integer $ q $ ( $ 1 \le q \le 2 \cdot 10^5 $ ) — number of points to check. Next $ q $ lines contain two integers per line: $ x_i $ and $ y_i $ ( $ 1 \le x_i, y_i \le 10^9 $ ) — points to process.

Print $ q $ lines. The $ i $ -th line should contain one real number — total time of the $ i $ -th point being in the shade, while the light source is moving from $ (a, s_y) $ to the $ (b, s_y) $ . The answer is considered as correct if its absolute of relative error doesn't exceed $ 10^{-6} $ .

- The 1-st point is always in the shade; - the 2-nd point is in the shade while light source is moving from $ (3, -3) $ to $ (6, -3) $ ; - the 3-rd point is in the shade while light source is at point $ (6, -3) $ . - the 4-th point is in the shade while light source is moving from $ (1, -3) $ to $ (2.5, -3) $ and at point $ (6, -3) $ ; - the 5-th point is in the shade while light source is moving from $ (1, -3) $ to $ (2.5, -3) $ and from $ (5.5, -3) $ to $ (6, -3) $ ;