CF1017E The Supersonic Rocket

战争结束后，超音速火箭成为了最常见的公共交通工具。 每个超音速火箭由两个“引擎”组成。每个引擎是一组“能量源”。第一个引擎有 $n$ 个能量源，第二个引擎有 $m$ 个能量源。每个能量源可以表示为二维平面上的一个点 $(x_i, y_i)$。每个引擎内的所有点都不相同。 你可以分别对每个引擎进行操作。每个引擎可以进行以下两种操作，每种操作可以执行任意多次。 1. 对该引擎的所有能量源整体平移：$(x_i, y_i)$ 变为 $(x_i+a, y_i+b)$，其中 $a$ 和 $b$ 可以是任意实数。也就是说，所有能量源会整体平移。 2. 对该引擎的所有能量源整体旋转：$(x_i, y_i)$ 变为 $(x_i \cos \theta - y_i \sin \theta, x_i \sin \theta + y_i \cos \theta)$，其中 $\theta$ 可以是任意实数。也就是说，所有能量源会整体旋转。 引擎的工作方式如下：当两个引擎启动后，它们的能量源会合并（此时不同引擎的能量源可能重合）。如果存在两个能量源 $A(x_a, y_a)$ 和 $B(x_b, y_b)$，那么对于所有满足 $0 < k < 1$ 的实数 $k$，会生成一个新的能量源 $C_k(kx_a + (1-k)x_b, ky_a + (1-k)y_b)$。然后，使用所有新旧能量源重复这一过程。最终，会生成所有能量源形成的“能量场”（可以看作是所有出现过的能量源的无限集合）。 如果经过你对引擎的操作后，任意删除一个能量源并再次启动引擎，所生成的能量场与未删除任何能量源时相同，则称该超音速火箭是“安全”的。只有当两个能量场中的任意一个能量源都属于另一个能量场时，才认为两个能量场相同。 给定一个超音速火箭，判断它是否安全。

第一行包含两个整数 $n$ 和 $m$（$3 \le n, m \le 10^5$），分别表示每个引擎的能量源数量。 接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$0 \leq x_i, y_i \leq 10^8$），表示第一个引擎的第 $i$ 个能量源的坐标。 再接下来的 $m$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$0 \leq x_i, y_i \leq 10^8$），表示第二个引擎的第 $i$ 个能量源的坐标。 保证每个引擎内不存在两个或以上位于同一点的能量源。

如果该超音速火箭是安全的，输出 "YES"；否则输出 "NO"。 你可以以任意大小写输出每个字母。

第一个样例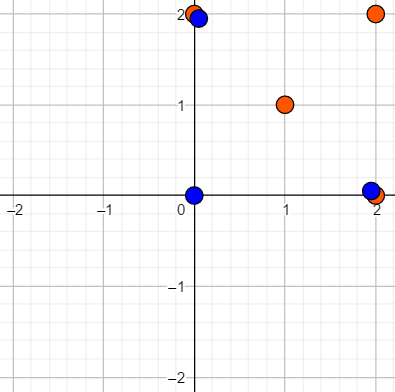：  图中靠近的蓝色和橙色点实际上是重合的。首先，对第一个引擎进行操作：使用第二种操作，取 $\theta = \pi$（即将所有能量源旋转 $180$ 度）。 第一个引擎的能量源变为 $(0, 0)$、$(0, -2)$ 和 $(-2, 0)$。 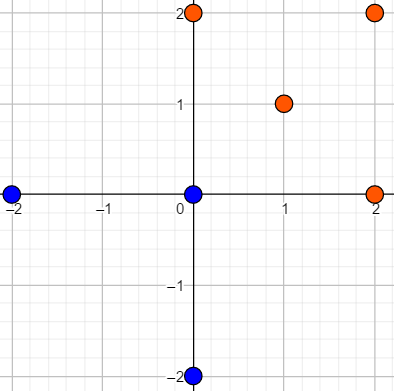 然后，对第二个引擎进行操作：使用第一种操作，取 $a = b = -2$。 第二个引擎的能量源变为 $(-2, 0)$、$(0, 0)$、$(0, -2)$ 和 $(-1, -1)$。 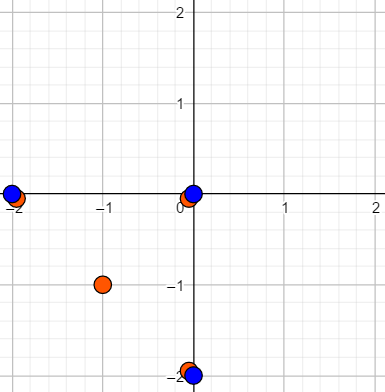 你可以验证，无论删除哪一个点，由两个引擎形成的能量场始终是由 $(0, 0)$、$(-2, 0)$、$(0, -2)$ 组成的实心三角形。 在第二个样例中，无论如何操作引擎，总存在第二个引擎中的某个能量源，使得删除它后能量场会缩小。 由 ChatGPT 4.1 翻译