CF1019C Sergey's problem

Sergey 五岁了！当他一岁的时候，他的父母给了他一个数；当他两岁的时候，他的父母给了他一个整数数组；三岁时他收到了一个字符串；当他四岁时，他的妈妈轻轻地叫醒他，让他做一个好孩子并给了他一棵有根树。今天是他的五岁生日！他收到了一份来自父母的有向图（没有自环）。 因为他很有好奇心，他决定找出一个集合 $Q$，使得其中的点两两之间没有连边，且对于不在集合中的任意一点 $v$ ，都存在集合内的一点 $u$ ，使得从 $u$ 出发，最多经过两条边就能到达 $v$ 。输出任意一组解。

第一行两个正整数 $n, m$（$1\leq n, m\leq 10 ^ 6$）表示图的点数和边数。 接下来 $m$ 行每行两个整数 $a, b$（$1\leq a, b\leq n$，$a\neq b$）表示 $a$ 到 $b$ 有一条有向边，可能有重边。

第一行输出整数 $k$ 表示集合中有 $k$ 个点。 第二行输出 $k$ 个整数表示集合中的点。保证有解。

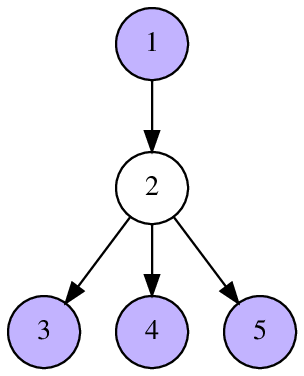
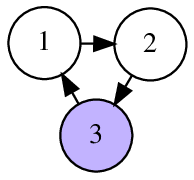
In the first sample, the vertices $ 1, 3, 4, 5 $ are not connected. The vertex $ 2 $ is reachable from vertex $ 1 $ by one edge. In the second sample, it is possible to reach the vertex $ 1 $ in one move and the vertex $ 2 $ in two moves. The following pictures illustrate sample tests and their answers.