CF1020A New Building for SIS

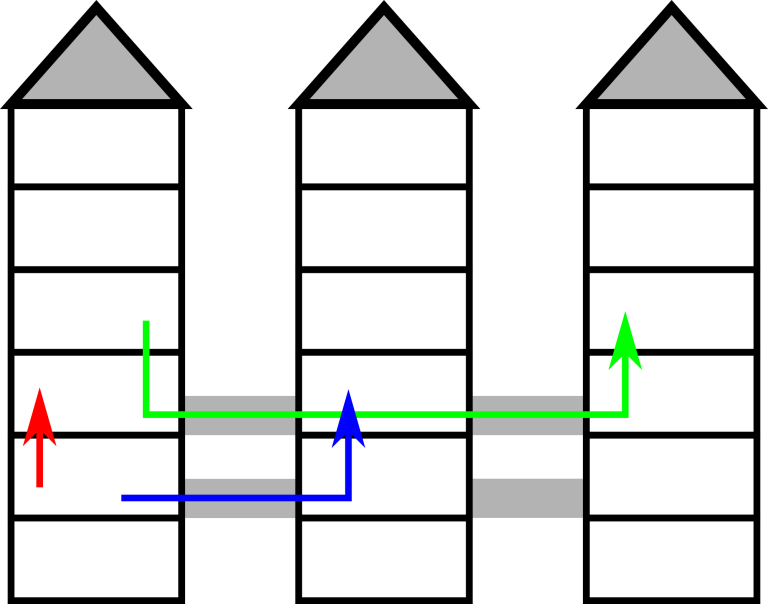
你正在研究夏季信息学院新建筑的楼层设计。因为你担任着英国秘密情报局的后勤物流任务，所以你十分在乎去往不同位置的路程耗时：了解从演讲室到食堂，或者从健身房到服务器机房的耗时是很重要的。 这个建筑由 $n$ 个塔楼组成，标号为 $1 - n$ ；每个塔楼有 $h$ 层，标号为 $1 - h$ 。任意两个相邻的塔楼间有一条通道（当 $1 \le i \le n - 1$ 时，塔楼 $i$ 与 $i - 1$ 相连）。在第 $x ( a \le x \le b)$ 层上，你可以在与第 $x$ 层相邻的2层移动，或如果第 $x$ 层与相邻的塔楼有通道连通也可移动至其上。离开建筑是不被允许的。  这个图片解释了 **输入 #1** 你将被给予 $k$ 对位置 $(t_a, f_a), (t_b, f_b)$ ：代表塔楼 $t_a$ 上的第 $f_a$ 层，塔楼 $t_b$ 上的第 $f_b$ 层。 对于每一对位置，你需要确定它们之间的最短耗时。

输入的第一行包含以下整数： - $n$ : 建筑中塔楼的个数 $(1 \le n \le 10^8)$ - $h$ : 塔楼的层数 $( 1 \le h \le 10^8)$ - $a$ 和 $b$ : 可以在相邻塔楼间移动的最低与最高楼层限制 $(1 \le a \le b \le h)$ - $k$ : 给予的位置个数 $ (1 \le k \le 10^4) $ 接下来 $k$ 行，是每对位置的详细数据，每对数据包括四个整数 $t_a, f_a, t_b, f_b (1 \le t_a, t_b \le n, 1 \le f_a, f_b \le h)$ 你需要确定它们间的最短耗时。

对于每对位置，回应一个整数，为两地之间最短路程耗时。