CF1023E Down or Right

这是一个交互题。 Bob 住在一个 $n \times n$ 的正方形网格中，行编号从上到下为 $1$ 到 $n$，列编号从左到右为 $1$ 到 $n$。每个格子要么是允许通过的，要么是被阻塞的，但你并不知道网格的具体情况。你只知道一个整数 $n$。 Bob 只能在允许通过的格子中移动，并且只能向下或向右移动到相邻的格子（前提是该格子允许通过）。 你最多可以询问 $4 \cdot n$ 次，询问的格式为 "? $r_1$ $c_1$ $r_2$ $c_2$"（$1 \le r_1 \le r_2 \le n$，$1 \le c_1 \le c_2 \le n$）。如果 Bob 能够从格子 $(r_1, c_1)$ 走到格子 $(r_2, c_2)$，则回答为 "YES"；否则回答为 "NO"。特别地，如果两个格子中有任意一个是被阻塞的，那么答案一定是 "NO"。由于 Bob 不喜欢短距离旅行，你只能询问曼哈顿距离不少于 $n-1$ 的两点对，即必须满足 $(r_2 - r_1) + (c_2 - c_1) \ge n - 1$。 保证 Bob 一定可以从左上角 $(1, 1)$ 走到右下角 $(n, n)$，你的任务是找到一条这样的路径。你需要以 "! S" 的形式输出答案，其中 $S$ 是一个长度为 $2n-2$ 的字符串，仅包含字符 'D' 和 'R'，分别表示向下和向右移动。向下移动会使第一维加 $1$，向右移动会使第二维加 $1$。如果有多种方案，任意一种都可以。输出答案后应立即结束程序。

输入的唯一一行包含一个整数 $n$（$2 \le n \le 500$），表示网格的大小。

当你准备好输出答案时，输出一行 "! S"，其中 $S$ 是一个长度为 $2n-2$ 的字符串，仅包含字符 'D' 和 'R'，表示从 $(1, 1)$ 到 $(n, n)$ 的一条合法路径，只经过允许通过的格子。

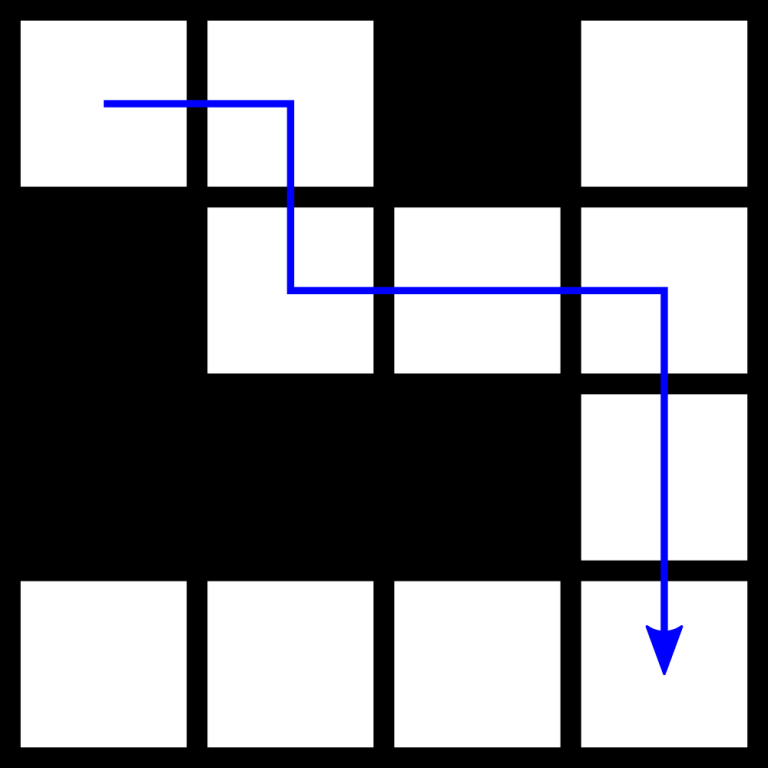
第一个样例如下图所示。  对于 hack 数据，输入格式如下： 第一行包含一个整数 $n$（$2 \le n \le 500$），表示网格的大小。 接下来的 $n$ 行，每行包含 $n$ 个字符，'#' 表示被阻塞的格子，'.' 表示允许通过的格子。 例如，下面的文本描述了上图的样例： ``` 4 ..#. #... ###. .... ``` 由 ChatGPT 4.1 翻译