CF1023G Pisces

一组研究人员正在研究一个由湖泊和河流组成的自然水系中的鱼类数量。该水系包含 $n$ 个湖泊，通过 $n-1$ 条河流相连。每条河流的长度（以千米为单位）为整数，并且可以双向通行。可以通过穿越河流在任意两个湖泊之间旅行（即湖泊和河流构成了一棵树）。 湖泊中生活着若干条无法区分的鱼，但具体数量未知。在第 $1$ 天，鱼可以位于任意湖泊。鱼可以通过游过河流在湖泊之间移动。每条鱼可以以 $l$ 天的时间游过长度为 $l$ 千米的河流，方向不限。此外，每条鱼可以在其到访的任意湖泊中停留任意天数。湖泊系统中不会有鱼凭空出现或消失。每个湖泊在任意时刻都可以容纳任意数量的鱼。 研究人员进行了若干次观测。第 $j$ 次观测的内容为：“在第 $d_j$ 天，湖泊 $p_j$ 至少有 $f_j$ 条不同的鱼”。请帮助研究人员确定不与观测结果矛盾的最小可能鱼的总数。

第一行包含一个整数 $n$（$1 \leq n \leq 10^5$），表示湖泊的数量。 接下来的 $n-1$ 行描述河流。第 $i$ 行包含三个整数 $u_i$、$v_i$、$l_i$（$1 \leq u_i, v_i \leq n$，$u_i \neq v_i$，$1 \leq l_i \leq 10^3$），表示第 $i$ 条河流连接湖泊 $u_i$ 和 $v_i$，长度为 $l_i$ 千米。 接下来一行包含一个整数 $k$（$1 \leq k \leq 10^5$），表示观测次数。 接下来的 $k$ 行描述观测。第 $j$ 行包含三个整数 $d_j$、$f_j$、$p_j$（$1 \leq d_j \leq 10^8$，$1 \leq f_j \leq 10^4$，$1 \leq p_j \leq n$），表示第 $j$ 次观测在第 $d_j$ 天、湖泊 $p_j$ 至少有 $f_j$ 条不同的鱼。任意两次观测不会在同一天同一个湖泊同时发生。

输出一个整数，表示不与观测结果矛盾的最小鱼的总数。

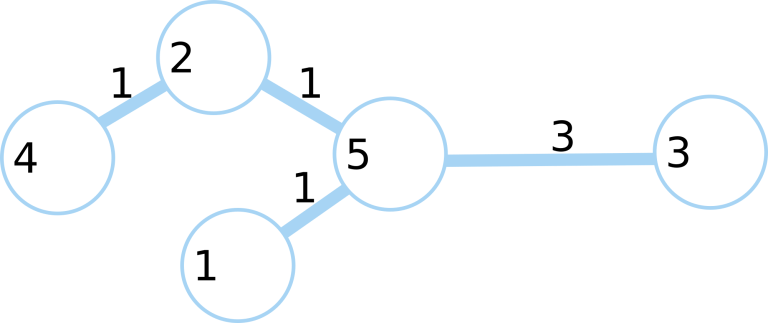
在第一个样例中，可以有一条鱼依次游经湖泊 $2$、$1$、$4$，另一条鱼依次游经湖泊 $3$、$1$、$2$。 在第二个样例中，一条鱼无法同时满足所有观测，但两条鱼分别游经 $2 \to 1 \to 4$ 和 $3 \to 1 \to 5$ 可以满足。 在第三个样例中，可以有一条鱼从湖泊 $1$ 游到湖泊 $5$，其余鱼在各自湖泊停留：湖泊 $4$ 有两条鱼，湖泊 $5$ 有六条鱼，湖泊 $3$ 有一条鱼。湖泊系统如图所示。  由 ChatGPT 4.1 翻译