CF1025F Disjoint Triangles

一个点属于一个三角形，当且仅当它在三角形内部或在三角形的某一条边上。如果平面上不存在任何一个点同时属于两个三角形，则称这两个三角形是互不相交的。 给定平面上的 $n$ 个点。任意两点不重合，且任意三点不共线。 请你计算，从这些点中选出两个互不相交的三角形的不同方案数。仅三角形的顺序不同或三角形内部顶点的顺序不同的两种方案视为相同。

输入的第一行包含一个整数 $n$（$6 \le n \le 2000$），表示点的数量。 接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$|x_i|, |y_i| \le 10^9$），表示一个点的坐标。 任意两点不重合，且任意三点不共线。

输出一个整数，表示选出两个互不相交的三角形的方案数。

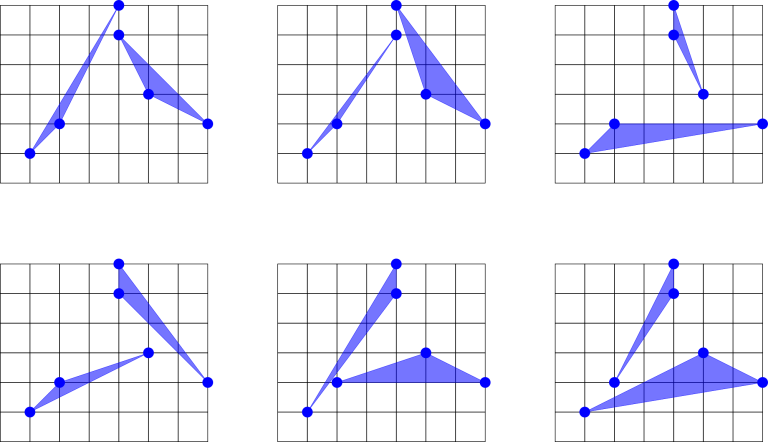
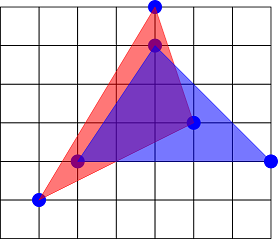
在第一个样例中，有六对互不相交的三角形，如下图所示。  所有其他的三角形对都不是互不相交的，例如下图中的三角形对：  由 ChatGPT 4.1 翻译