CF1025G Company Acquisitions
题目描述
有 $n$ 个初创公司。每个公司可以是活跃的或已被收购的。如果一个公司被收购了,说明它正好跟随一个活跃的公司。一个活跃的公司可以被任意多个已被收购的公司跟随。活跃的公司不能跟随其他公司。
以下过程会一直进行,直到只剩下一个活跃的公司。每次执行下列步骤需要恰好 1 天:
1. 随机等概率选出两个不同的活跃公司 $A$ 和 $B$。
2. 掷一次公平的硬币,等概率地决定 $A$ 收购 $B$ 或 $B$ 收购 $A$(即如果 $A$ 收购 $B$,那么 $B$ 的状态从活跃变为已被收购,并开始跟随 $A$)。
3. 当一个公司从活跃变为已被收购时,它之前所有已被收购的下属公司都会变为活跃状态。
例如,可能出现如下情形:假设 $A$、$B$ 是活跃公司,$C$、$D$、$E$ 是 $A$ 的已被收购公司,$F$、$G$ 是 $B$ 的已被收购公司:

红色表示活跃公司。
如果 $A$ 收购 $B$,则状态变为 $A$、$F$、$G$ 是活跃公司,$C$、$D$、$E$、$B$ 是 $A$ 的已被收购公司,$F$ 和 $G$ 没有下属:
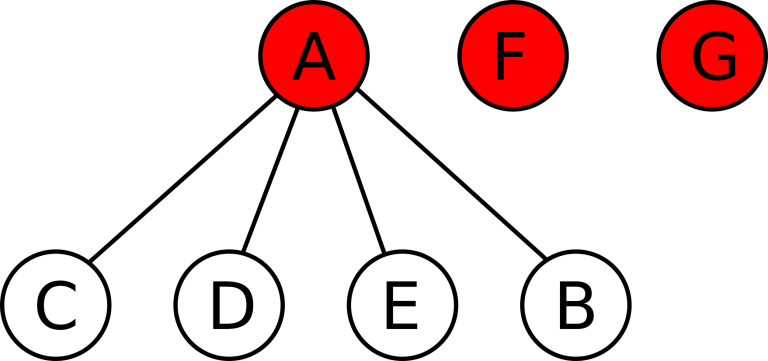
如果反过来 $B$ 收购 $A$,则状态变为 $B$、$C$、$D$、$E$ 是活跃公司,$F$、$G$、$A$ 是 $B$ 的已被收购公司,$C$、$D$、$E$ 没有下属:
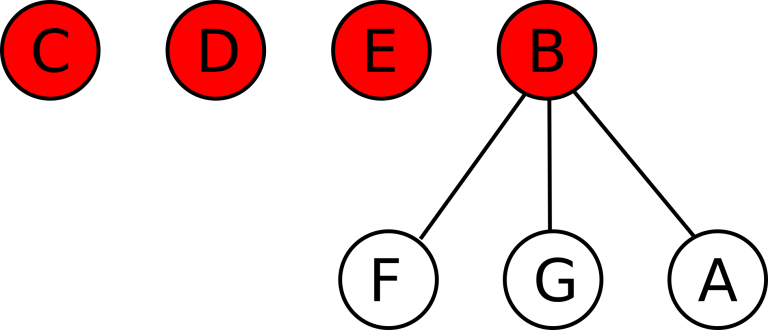
现在给定初创公司的初始状态。对于每个公司,告知其是活跃还是已被收购。如果是已被收购,还会给出它当前跟随的活跃公司的编号。
你需要计算,最终只剩下一个活跃公司时,所需天数的期望值。
可以证明,期望天数可以表示为有理数 $P/Q$,其中 $P$ 和 $Q$ 是互质整数,且 $Q \not= 0 \pmod{10^9+7}$。请输出 $P \cdot Q^{-1}$ 模 $10^9+7$ 的结果。
输入格式
第一行包含一个整数 $n$($2 \leq n \leq 500$),表示初创公司的数量。
第二行包含 $n$ 个用空格分隔的整数 $a_1, a_2, \ldots, a_n$($a_i = -1$ 或 $1 \leq a_i \leq n$)。如果 $a_i = -1$,表示公司 $i$ 是活跃的。否则,如果 $1 \leq a_i \leq n$,表示公司 $i$ 已被收购,且当前跟随公司 $a_i$。保证如果 $a_i \not= -1$,则 $a_{a_i} = -1$(即所有被跟随的公司都是活跃的)。
输出格式
输出一个整数,表示最终只剩下一个活跃公司所需天数的期望值,模 $10^9+7$。
说明/提示
在第一个样例中,有三个活跃公司,编号为 $1$、$2$ 和 $3$,没有已被收购的公司。以下是可能发生的一种情况:
1. 公司 $1$ 收购公司 $2$(此时状态为 $[-1, 1, -1]$)
2. 公司 $3$ 收购公司 $1$(此时状态为 $[3, -1, -1]$)
3. 公司 $2$ 收购公司 $3$(此时状态为 $[-1, -1, 2]$)
4. 公司 $2$ 收购公司 $1$(此时状态为 $[2, -1, 2]$)
此时只剩下一个活跃公司,整个过程共花费 $4$ 天。可以证明期望天数为 $3$。
第二个样例中,只有一个活跃公司,因此需要 $0$ 天。
最后一个样例中,记得对答案取模 $10^9+7$。
由 ChatGPT 4.1 翻译