CF1029F Multicolored Markers

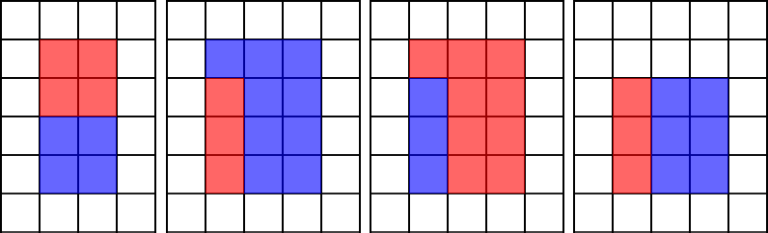
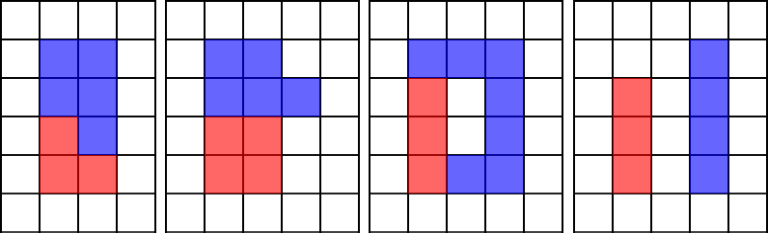
有一个无限大的方格棋盘，初始时所有格子都是白色的。 Vova 有一支红色记号笔和一支蓝色记号笔。红色记号笔可以涂色 $a$ 个格子，蓝色记号笔可以涂色 $b$ 个格子。如果某个格子不是白色，则不能再用任何颜色的记号笔涂色。每支记号笔都必须完全用完，因此最终棋盘上恰好有 $a$ 个红色格子和 $b$ 个蓝色格子。 Vova 想要涂色一组格子，使得： - 这些格子组成一个矩形，且恰好有 $a+b$ 个被涂色的格子； - 至少有一种颜色的所有格子也组成一个矩形。 以下是一些合法的涂色示例：  以下是一些不合法的涂色示例：  在所有合法的涂色方案中，Vova 想选择周长最小的那种。请问 Vova 能获得的最小周长是多少？ 保证至少存在一种合法的涂色方案。

一行包含两个整数 $a$ 和 $b$（$1 \le a, b \le 10^{14}$），分别表示红色记号笔和蓝色记号笔应涂色的格子数。

输出一个整数，表示 Vova 通过恰好涂色 $a$ 个红色格子和 $b$ 个蓝色格子所能获得的最小矩形周长。 保证至少存在一种合法的涂色方案。

前四个示例对应题面中的第一张图片。 注意，对于所有示例，都存在多种合法的涂色方案。 在第一个示例中，你也可以构造一个边长为 $1$ 和 $8$ 的矩形，但其周长为 $18$，比 $8$ 要大。 在第二个示例中，你可以构造一个边长为 $3$ 和 $4$ 的矩形，但红色格子会组成边长为 $1$ 和 $3$ 的矩形，蓝色格子会组成边长为 $3$ 和 $3$ 的矩形。 由 ChatGPT 4.1 翻译