CF1030D Vasya and Triangle

Vasya 有三个整数 $n$、$m$ 和 $k$。他想找到三个整数点 $(x_1, y_1)$、$(x_2, y_2)$、$(x_3, y_3)$，使得 $0 \le x_1, x_2, x_3 \le n$，$0 \le y_1, y_2, y_3 \le m$，并且由这三点构成的三角形的面积等于 $\frac{nm}{k}$。 请帮助 Vasya！找到满足条件的点（如果存在）。如果有多组解，输出任意一组即可。

一行包含三个整数 $n$、$m$、$k$，满足 $1 \le n, m \le 10^9$，$2 \le k \le 10^9$。

如果不存在这样的点，输出 "NO"。 否则，第一行输出 "YES"。接下来的三行，每行输出一组点的坐标 $x_i, y_i$，每行一个点。如果有多组解，输出任意一组即可。 输出中的字母大小写均可。

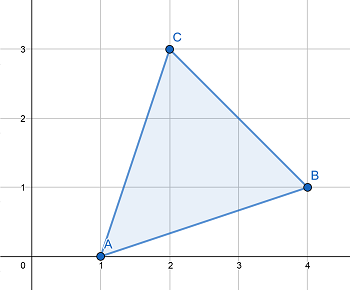
在第一个样例中，三角形的面积应为 $\frac{nm}{k} = 4$。输出中的三角形如下图所示：  在第二个样例中，不存在面积为 $\frac{nm}{k} = \frac{16}{7}$ 的三角形。 由 ChatGPT 4.1 翻译