CF1030D Vasya and Triangle

Vasya has got three integers $ n $ , $ m $ and $ k $ . He'd like to find three integer points $ (x_1, y_1) $ , $ (x_2, y_2) $ , $ (x_3, y_3) $ , such that $ 0 \le x_1, x_2, x_3 \le n $ , $ 0 \le y_1, y_2, y_3 \le m $ and the area of the triangle formed by these points is equal to $ \frac{nm}{k} $ . Help Vasya! Find such points (if it's possible). If there are multiple solutions, print any of them.

The single line contains three integers $ n $ , $ m $ , $ k $ ( $ 1\le n, m \le 10^9 $ , $ 2 \le k \le 10^9 $ ).

If there are no such points, print "NO". Otherwise print "YES" in the first line. The next three lines should contain integers $ x_i, y_i $ — coordinates of the points, one point per line. If there are multiple solutions, print any of them. You can print each letter in any case (upper or lower).

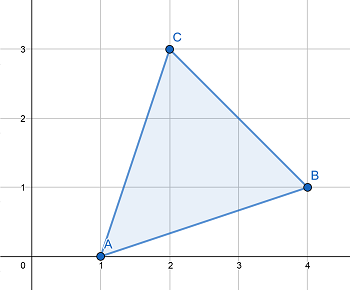In the first example area of the triangle should be equal to $ \frac{nm}{k} = 4 $ . The triangle mentioned in the output is pictured below: In the second example there is no triangle with area $ \frac{nm}{k} = \frac{16}{7} $ .