CF1032D Barcelonian Distance

在本题中，我们考虑一个极为简化的巴塞罗那城市模型。 巴塞罗那可以被表示为一个平面，其中每个整数 $c$ 都有一条 $x = c$ 和 $y = c$ 的街道（即矩形网格）。然而，有一个细节使得巴塞罗那不同于曼哈顿：有一条名为 Avinguda Diagonal 的大道，可以表示为满足 $ax + by + c = 0$ 的所有点的集合。 你可以沿着这些街道行走，包括这条大道。现在给定巴塞罗那某处的两个整数点 $A$ 和 $B$，请你求出从 $A$ 到 $B$ 需要行走的最小距离。

第一行包含三个整数 $a$、$b$ 和 $c$（$-10^9 \leq a, b, c \leq 10^9$，且 $a$ 和 $b$ 至少有一个不为零），表示对角大道的方程。 第二行包含四个整数 $x_1$、$y_1$、$x_2$ 和 $y_2$（$-10^9 \leq x_1, y_1, x_2, y_2 \leq 10^9$），表示点 $A = (x_1, y_1)$ 和 $B = (x_2, y_2)$。

输出从 $A$ 到 $B$ 的最小可能行走距离。你的答案被认为是正确的，当且仅当其绝对误差或相对误差不超过 $10^{-6}$。 形式化地，设你的答案为 $a$，标准答案为 $b$，当且仅当 $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}$ 时，你的答案才会被接受。

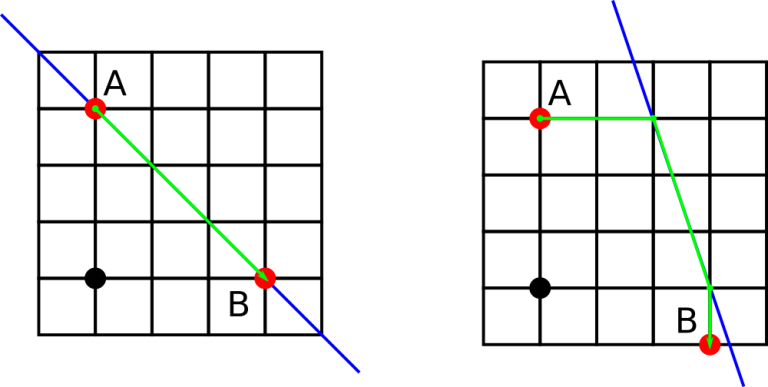
第一个样例见下图左侧，第二个样例见下图右侧。蓝色为大道，黑点为原点。  由 ChatGPT 4.1 翻译