CF1036A Function Height

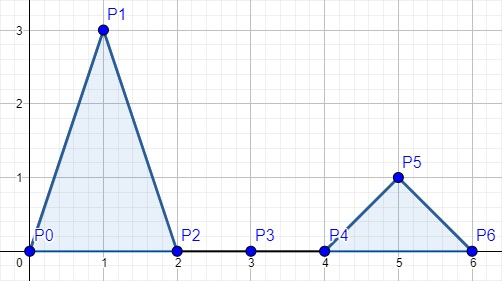
给定平面直角坐标系上的 $2n+1$ 个整点，这些点从 $0$ 到 $2n$ 编号。设 $P_i$ 为第 $i$ 个点。点 $P_i$ 的 $x$ 坐标为 $i$，$y$ 坐标初始为 $0$，即 $P_i = (i, 0)$。 这些点是一段分段函数图像的顶点。第 $j$ 段函数是连接 $P_j$ 和 $P_{j+1}$ 的线段。 每次操作，你可以将任意 $x$ 坐标为奇数的点（即 $P_1, P_3, \dots, P_{2n-1}$）的 $y$ 坐标增加 $1$。注意，相应的线段也会随之变化。 例如，下图展示了 $n=3$（即点的数量为 $2 \cdot 3 + 1 = 7$）的一个函数图像，其中 $P_1$ 的 $y$ 坐标增加了 $3$ 次，$P_5$ 的 $y$ 坐标增加了 $1$ 次：  定义图像的面积为该图像下方、$OX$ 坐标轴上方的面积。例如，上图中浅蓝色部分的面积为 $4$。 定义图像的高度为所有顶点（即 $P_0, P_1, \dots, P_{2n}$）中最大的 $y$ 坐标。上图中图像的高度为 $3$。 你的任务是，对于由 $2n+1$ 个顶点组成且面积为 $k$ 的图像，求其最小可能高度。注意，不需要最小化操作次数。 可以证明，按照上述操作得到的任何答案总是存在，并且是一个不超过 $10^{18}$ 的整数。

输入第一行包含两个整数 $n$ 和 $k$（$1 \le n, k \le 10^{18}$），分别表示分段函数的顶点数和所需的面积。

输出一个整数，表示由 $2n+1$ 个顶点组成且面积为 $k$ 的图像的最小可能高度。可以证明，按照上述操作得到的任何答案总是存在，并且是一个不超过 $10^{18}$ 的整数。

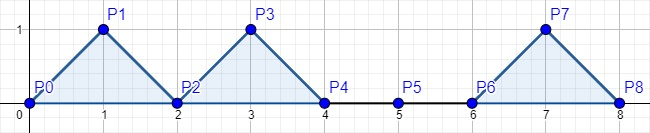
第一个样例的一个可能答案如下：  该图像的面积为 $3$，高度为 $1$。 第二个样例只有唯一的答案：  该图像的面积为 $12$，高度为 $3$。 由 ChatGPT 4.1 翻译