CF1036E Covered Points

给定 $n$ 条线段，位于笛卡尔平面上。每条线段的两个端点的坐标均为整数。线段之间可以相交，但没有两条线段共线。 请你统计有多少个不同的整点（即横纵坐标均为整数的点）被至少一条线段覆盖。

第一行包含一个整数 $n$（$1 \le n \le 1000$），表示线段的数量。 接下来的 $n$ 行，每行包含四个整数 $Ax_i, Ay_i, Bx_i, By_i$（$-10^6 \le Ax_i, Ay_i, Bx_i, By_i \le 10^6$），表示第 $i$ 条线段的两个端点 $A$ 和 $B$ 的坐标（$A \ne B$）。 保证没有两条线段共线。

输出一个整数，表示被至少一条线段覆盖的不同整点的数量。

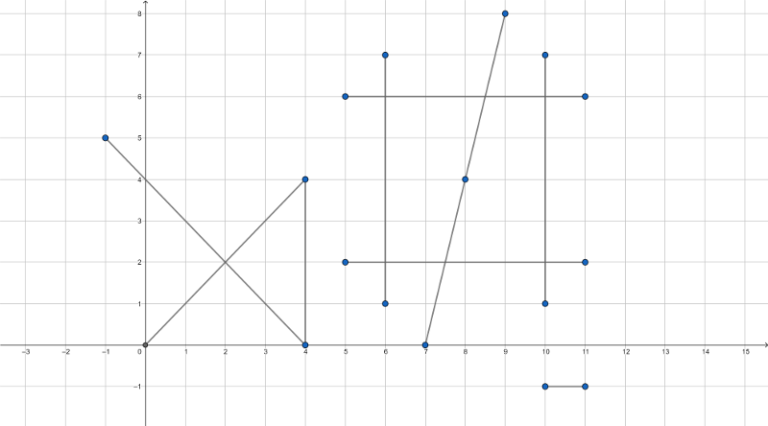
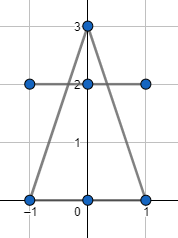
第一个样例的示意图如下：  图中蓝色标记了一些关键点，答案还包含了一些未标记的点。 第二个样例的示意图如下：  由 ChatGPT 4.1 翻译