CF1039D You Are Given a Tree
题目描述
一棵树是一个其中每对顶点之间恰好有一条简单路径的无向图。我们称一组简单路径为 $k$-可行集,当且仅当树中的每个顶点至多属于其中一条路径(包括端点),且每条路径恰好包含 $k$ 个顶点。
给定一棵有 $n$ 个顶点的树。对于每个 $k$($1 \leq k \leq n$),求 $k$-可行集的最大可能大小。
输入格式
输入的第一行包含一个整数 $n$($2 \leq n \leq 100\,000$),表示树的顶点数。
接下来的 $n-1$ 行描述这棵树,每行包含两个整数 $v,u$($1 \leq v, u \leq n$),表示一条边的两个端点。
保证给定的图是一棵树。
输出格式
输出 $n$ 个数字,第 $i$ 个数字表示 $i$-可行集的最大可能大小。
说明/提示
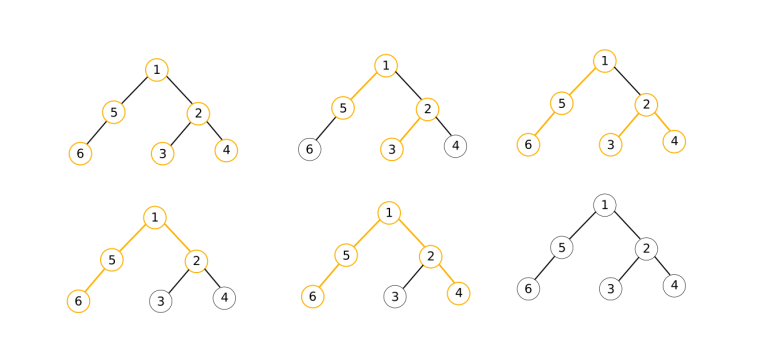
对于第二个样例,一种达到最优路径数量的方法如下图所示: