CF1039D You Are Given a Tree

A tree is an undirected graph with exactly one simple path between each pair of vertices. We call a set of simple paths $ k $ -valid if each vertex of the tree belongs to no more than one of these paths (including endpoints) and each path consists of exactly $ k $ vertices. You are given a tree with $ n $ vertices. For each $ k $ from $ 1 $ to $ n $ inclusive find what is the maximum possible size of a $ k $ -valid set of simple paths.

The first line of the input contains a single integer $ n $ ( $ 2 \le n \le 100\,000 $ ) — the number of vertices in the tree. Then following $ n - 1 $ lines describe the tree, each of them contains two integers $ v $ , $ u $ ( $ 1 \le v, u \le n $ ) — endpoints of the corresponding edge. It is guaranteed, that the given graph is a tree.

Output $ n $ numbers, the $ i $ -th of which is the maximum possible number of paths in an $ i $ -valid set of paths.

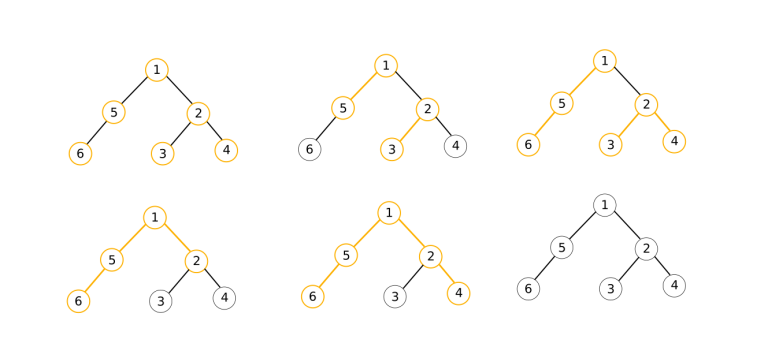
One way to achieve the optimal number of paths for the second sample is illustrated in the following picture: