CF1042F Leaf Sets

给定一棵包含 $n$ 个顶点的无向树。 如果某个顶点恰好与一个顶点相邻，则称其为叶子节点。 两个顶点之间的距离定义为它们之间最短路径上的边数。 我们称一组叶子节点为“美丽集合”，如果该集合中任意两叶子节点之间的最大距离不超过 $k$。 你需要将所有叶子节点划分为若干个互不相交的美丽集合。请问最少需要多少个美丽集合？

第一行包含两个整数 $n$ 和 $k$（$3 \le n \le 10^6$，$1 \le k \le 10^6$），分别表示树的顶点数和每个美丽集合中任意两叶子节点之间的最大距离。 接下来的 $n-1$ 行，每行包含两个整数 $v_i$ 和 $u_i$（$1 \le v_i, u_i \le n$），表示第 $i$ 条边的两个端点。 保证所给边构成一棵树。

输出一个整数，表示最少需要多少个美丽集合。

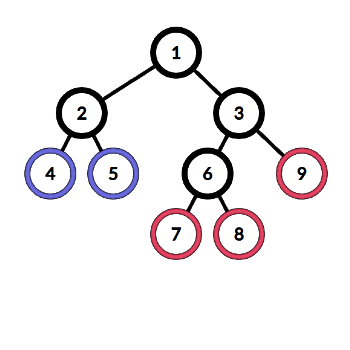
以下是第一个样例的图示：  由 ChatGPT 4.1 翻译