CF1044A The Tower is Going Home

在一个宽度为 $10^9$、高度为 $10^9$ 的棋盘上，行号自下而上从 $1$ 到 $10^9$，列号自左而右从 $1$ 到 $10^9$。因此，每个格子都可以用坐标 $(x, y)$ 表示，其中 $x$ 是列号，$y$ 是行号。 每天，黑白棋子都会在这块棋盘上激烈厮杀。今天，黑方获胜，但付出了惨重的代价——只剩下一只车存活下来，并且被逼到了左下角的格子 $(1,1)$。不过它依然很高兴，因为胜利属于它，现在是时候庆祝了！为了庆祝，车需要回家，也就是到达棋盘的最上边（即任意一个行号为 $10^9$ 的格子）。 本来一切都很顺利，但狡猾的白棋子在比赛结束前对棋盘上的某些位置施加了魔法。魔法分为两种类型： - 垂直魔法。每个垂直魔法由一个数字 $x$ 定义。这样的魔法会在第 $x$ 列和第 $x+1$ 列之间制造一条无限阻挡线。 - 水平魔法。每个水平魔法由三个数字 $x_1$、$x_2$、$y$ 定义。这样的魔法会在第 $y$ 行、第 $x_1$ 列到第 $x_2$ 列（包含两端）之间的格子上方制造一段阻挡线。这类魔法有个特点：任意两条水平魔法线段不会有公共点。注意，水平魔法可以与垂直魔法有公共点。  我们再回顾一下，车是一种可以在一步内移动到同一行或同一列任意位置的棋子。在本题中，车可以从格子 $(r_0, c_0)$ 移动到格子 $(r_1, c_1)$，前提是 $r_1 = r_0$ 或 $c_1 = c_0$，并且这两个格子之间没有阻挡线或阻挡段（具体可参考样例）。 幸运的是，车可以移除魔法，但这需要付出极大的努力。因此，它希望移除的魔法数量尽可能少，使得它能够回家。请你计算，车最少需要移除多少个魔法，才能从 $(1,1)$ 到达至少一个行号为 $10^9$ 的格子。

第一行包含两个整数 $n$ 和 $m$（$0 \le n, m \le 10^5$），分别表示垂直魔法和水平魔法的数量。 接下来的 $n$ 行，每行包含一个整数 $x$（$1 \le x < 10^9$），表示一个垂直魔法。它会在第 $x$ 列和第 $x+1$ 列之间制造一条阻挡线。 接下来的 $m$ 行，每行包含三个整数 $x_1$、$x_2$ 和 $y$（$1 \le x_1 \le x_2 \le 10^9$，$1 \le y < 10^9$），表示一个水平魔法。它会在第 $y$ 行、第 $x_1$ 列到第 $x_2$ 列（包含两端）之间的格子上方制造一段阻挡线。 保证所有魔法均不相同，且任意两条水平魔法线段不会有公共点。

输出一个整数，表示车最少需要移除多少个魔法，才能从 $(1,1)$ 到达至少一个行号为 $10^9$ 的格子。

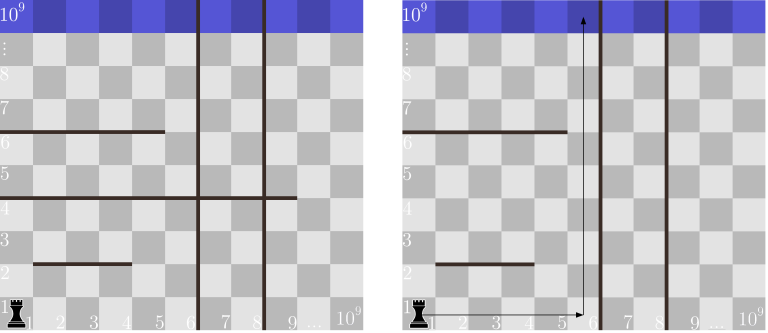
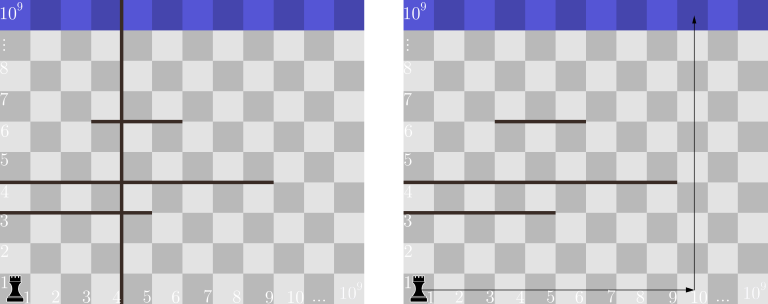
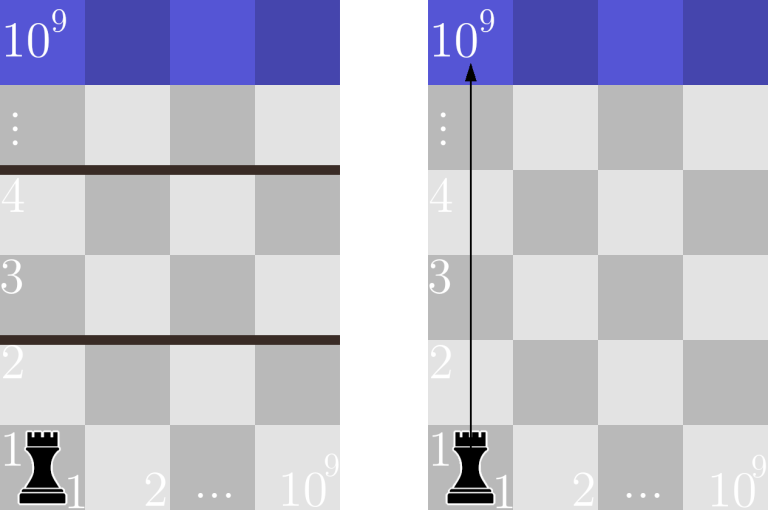
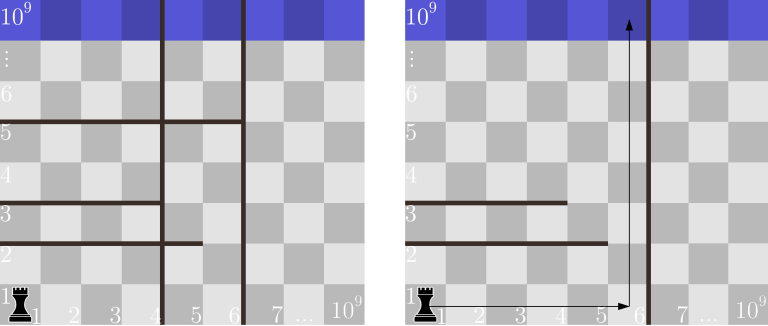
在第一个样例中，为了让车回家，只需移除第二个水平魔法。  在第二个样例中，只需移除唯一的垂直魔法。如果只移除某一个水平魔法，车依然无法回家，因为它会被剩下的水平魔法从上方阻挡，右侧又被垂直魔法阻挡。  在第三个样例中，有两条横跨整个棋盘的水平魔法，无法绕过，必须全部移除。  在第四个样例中，没有任何魔法，因此无需移除任何魔法。 在第五个样例中，可以移除第一个垂直魔法和第三个水平魔法。  由 ChatGPT 4.1 翻译