CF1044B Intersecting Subtrees

你正在和 Li Chen 玩一个奇怪的游戏。你们有一棵包含 $n$ 个节点的树画在纸上，所有节点都是无标号且可区分的。你们每个人都独立地将树的节点标号为 $1$ 到 $n$。你们彼此都不知道对方的标号方式。 你和 Li Chen 各自选择了树上的一个子树（即一个连通子图）。你的子树包含你标号下的 $x_1, x_2, \ldots, x_{k_1}$ 这些节点，Li Chen 的子树包含他标号下的 $y_1, y_2, \ldots, y_{k_2}$ 这些节点。$x_1, x_2, \ldots, x_{k_1}$ 和 $y_1, y_2, \ldots, y_{k_2}$ 的值你们双方都知道。 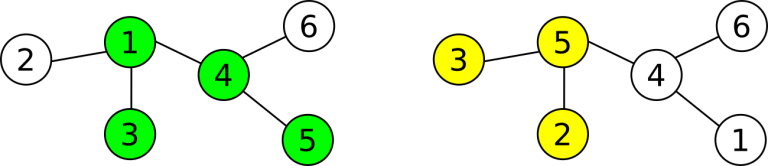 图中展示了同一棵树的两种标号方式：左侧是你的标号，右侧是 Li Chen 的标号。高亮部分是你们各自选择的子树。两棵子树有两个公共节点。 你想要判断你们的子树是否至少有一个公共节点。幸运的是，你的朋友 Andrew 同时知道你们两个人的标号方式。你最多可以向 Andrew 询问 $5$ 个问题，每个问题有以下两种形式之一： - A x：Andrew 会查看你标号下的节点 $x$，并告诉你该节点在 Li Chen 标号下的编号。 - B y：Andrew 会查看 Li Chen 标号下的节点 $y$，并告诉你该节点在你的标号下的编号。 请在询问一些问题后，判断你们的子树是否有至少一个公共节点。如果有，请输出你标号下的任意一个公共节点编号。

每个测试包含若干组数据。 第一行输入一个整数 $t$（$1 \leq t \leq 100$），表示测试用例的组数。 对于每组测试数据，交互格式如下： 第一行输入一个整数 $n$（$1 \leq n \leq 1000$），表示树的节点数。 接下来 $n-1$ 行，每行输入两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$），表示你标号下的树的边。 接下来一行输入一个整数 $k_1$（$1 \leq k_1 \leq n$），表示你的子树的节点数。 下一行输入 $k_1$ 个互不相同的整数 $x_1, x_2, \ldots, x_{k_1}$（$1 \leq x_i \leq n$），表示你标号下的子树节点编号。保证这些节点在你的标号下构成一棵子树。 接下来一行输入一个整数 $k_2$（$1 \leq k_2 \leq n$），表示 Li Chen 的子树的节点数。 下一行输入 $k_2$ 个互不相同的整数 $y_1, y_2, \ldots, y_{k_2}$（$1 \leq y_i \leq n$），表示 Li Chen 标号下的子树节点编号。保证这些节点在 Li Chen 的标号下构成一棵子树。 测试用例会逐个给出，因此你必须在完成当前测试用例的交互（即输出一个公共节点或 $-1$，如果没有公共节点）后，才能开始接收下一个测试用例。 你可以向 Andrew 询问两种不同类型的问题： - 你可以输出 "A x"（$1 \leq x \leq n$）。Andrew 会查看你标号下的节点 $x$，并回复该节点在 Li Chen 标号下的编号。 - 你可以输出 "B y"（$1 \leq y \leq n$）。Andrew 会查看 Li Chen 标号下的节点 $y$，并回复该节点在你的标号下的编号。 每棵树最多只能询问 $5$ 个问题。 当你准备好输出答案时，输出 "C s"，其中 $s$ 是你标号下的一个公共节点编号，如果没有公共节点则输出 $-1$。输出答案不计入问题次数。记得在输出后刷新输出缓冲区，以便接收下一个测试用例。 如果你询问次数超过限制，或询问了无效的问题，评测机会回复 $-1$，你的程序应立即终止（例如调用 exit(0)）。你会收到 Wrong Answer 判定；如果忽略此情况，程序继续读取已关闭的输入流，可能会收到其它判定。 Hack 格式 用于 Hack 的输入格式如下。注意只能用一组测试数据进行 Hack。 第一行输入一个整数 $t$（$t=1$）。 第二行输入一个整数 $n$（$1 \leq n \leq 1000$）。 第三行输入 $n$ 个整数 $p_1, p_2, \ldots, p_n$（$1 \leq p_i \leq n$），为 $1$ 到 $n$ 的一个排列。表示 Li Chen 对树的标号方式。即你标号下的第 $i$ 个节点在 Li Chen 的标号下为 $p_i$。 接下来 $n-1$ 行，每行输入两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$），表示树的边。 接下来一行输入一个整数 $k_1$（$1 \leq k_1 \leq n$）。 下一行输入 $k_1$ 个互不相同的整数 $x_1, x_2, \ldots, x_{k_1}$（$1 \leq x_i \leq n$），这些节点在你的标号下构成一棵子树。 接下来一行输入一个整数 $k_2$（$1 \leq k_2 \leq n$）。 下一行输入 $k_2$ 个互不相同的整数 $y_1, y_2, \ldots, y_{k_2}$（$1 \leq y_i \leq n$），这些节点在 Li Chen 的标号下构成一棵子树。

每组测试用例，你需要与评测机进行交互。 你可以最多询问 $5$ 个问题，每个问题格式如下： - "A x"：询问你标号下的节点 $x$ 在 Li Chen 标号下的编号。 - "B y"：询问 Li Chen 标号下的节点 $y$ 在你标号下的编号。 当你确定答案后，输出 "C s"，其中 $s$ 是你标号下的一个公共节点编号，如果没有公共节点则输出 $-1$。输出答案不计入问题次数。 每次输出后请刷新输出缓冲区。

对于第一个样例，Li Chen 的隐藏排列为 $[2, 3, 1]$，对于第二个样例，他的隐藏排列为 $[5, 3, 2, 4, 1, 6]$。 在第一个样例中，树为一条三节点的链。上方是你的标号和你选择的子树，下方是 Li Chen 的标号和他选择的子树： 在第一个问题中，你询问 Andrew 你标号下的节点 $1$ 在 Li Chen 标号下的编号，Andrew 回答 $2$。此时你知道你们的子树包含同一个节点（即你标号下的节点 $1$），所以你可以输出 "C 1" 并结束。当然，你也可以询问 Andrew Li Chen 标号下的节点 $2$ 在你标号下的编号，Andrew 回答 $1$（这一步只是为了演示如何提问）。 对于第二个样例，有两组测试数据。第一组如下图所示： 我们首先询问 "B 2"，Andrew 会告诉我们 $3$。此时我们知道 $3$ 是一个公共节点，而且任何包含节点 $3$ 的大小为 $3$ 的子树必然包含节点 $1$，所以我们可以输出 "C 1" 或 "C 3" 作为答案。 第二组测试数据如下： 在这种情况下，你知道唯一一个不包含节点 $1$ 的大小为 $3$ 的子树是 $4,5,6$。你询问 Andrew 你标号下的节点 $1$ 在 Li Chen 标号下的编号，Andrew 回答 $5$。此时你知道 Li Chen 的子树不包含节点 $1$，所以他的子树一定是 $4,5,6$（在你的标号下），因此两棵子树没有公共节点。 由 ChatGPT 4.1 翻译