CF1044E Grid Sort
题目描述
给你一个 $n \times m$ 的网格。网格的每个单元格内填充了从 $1$ 到 $nm$ 的唯一整数,每个整数只出现一次。
每次操作,你可以选择网格中的任意一个环,然后让这个环上的所有整数顺时针移动一个位置。一个“环”需要满足以下条件:
- 至少包含四个方格;
- 每个方格在环中至多出现一次;
- 每对相邻方格(包括第一个和最后一个方格)必须共享一个边。
例如,看下面的网格:
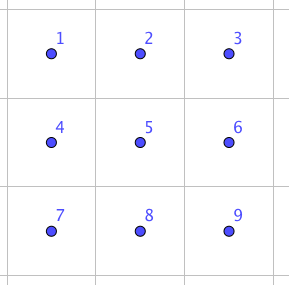
我们可以选择一个这样的环:
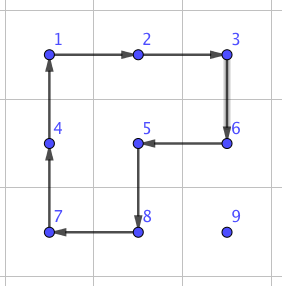
执行操作后得到的新网格是:
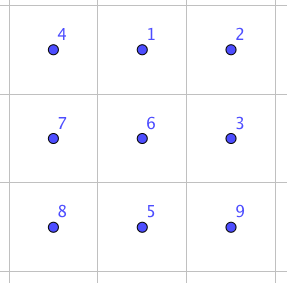
在此例中,所选择的环可以表示为序列 $[1, 2, 3, 6, 5, 8, 7, 4]$,数字按所希望的旋转方向排列。
请找到一系列操作,将网格有序化,使得从上到下连接每一行后形成的数组是排序好的(参见上面的第一张图)。
注意,不必追求最小化操作次数或环的总长度。惟一的要求是:所有环的长度总和不能超过 $10^5$。在当前约束条件下,可以保证总有解。你只需输出一个有效的步骤序列来实现网格的排序。
输入格式
第一行包含两个整数 $n$ 和 $m$($3 \leq n, m \leq 20$),表示网格的大小。
接下来的 $n$ 行中,每行包含 $m$ 个整数 $x_{i,1}, x_{i,2}, \ldots, x_{i, m}$($1 \leq x_{i,j} \leq nm$),表示第 $i$ 行第 $j$ 列的数值。
可以保证所有的 $x_{i,j}$ 都是不同的。
输出格式
首先输出一个整数 $k$,表示所需操作的次数($k \geq 0$)。
后面的 $k$ 行中,每行描述一个环,其格式如下:
$$ s\ y_1\ y_2\ \ldots\ y_s $$
其中,$s$ 表示要移动的方块的数量($s \geq 4$)。在这个环中,方块 $y_1$ 移动到方块 $y_2$ 的位置,方块 $y_2$ 移动到方块 $y_3$ 的位置,依此类推,最后一个方块 $y_s$ 移动到方块 $y_1$ 的位置。
所有操作中各个 $s$ 的总和不能超过 $10^5$。
**本翻译由 AI 自动生成**
说明/提示
The first sample is the case in the statement. Here, we can use the cycle in reverse order to sort the grid.