CF1044F DFS

给定一棵有 $n$ 个顶点的树 $T$。考虑一个初始等于 $T$ 的图 $G_0$。你将得到 $q$ 次操作，每次操作给出一对不同的整数 $u_i$ 和 $v_i$。 对于每一次操作 $i$（$1 \le i \le q$），我们定义图 $G_i$ 如下： - 如果 $G_{i-1}$ 包含边 $\{u_i, v_i\}$，则将其删除，得到 $G_i$。 - 否则，在 $G_{i-1}$ 中加入这条边，得到 $G_i$。 形式化地，$G_i := G_{i-1} \triangle \{\{u_i, v_i\}\}$，其中 $\triangle$ 表示[对称差](https://en.wikipedia.org/wiki/Symmetric_difference)。 此外，保证 $T$ 始终是 $G_i$ 的子图。换句话说，操作不会删除 $T$ 中的边。 考虑一个连通图 $H$，对其进行一次深度优先搜索（DFS）。可以发现，遍历过程中访问到尚未访问的顶点所经过的边（即树边）会构成 $H$ 的一棵生成树。对于同一个图，这棵生成树通常不是唯一的——它依赖于起始顶点以及每个顶点邻居的遍历顺序。 我们称顶点 $w$ 是“好”的，如果存在一种邻居遍历顺序，使得从 $w$ 开始的 DFS 生成的生成树恰好为 $T$。对于每次操作 $i$（$1 \le i \le q$），请你求出当前图中“好”顶点的数量。

第一行包含两个整数 $n$ 和 $q$（$3 \le n \le 2 \cdot 10^5$，$1 \le q \le 2 \cdot 10^5$），分别表示节点数和操作次数。 接下来 $n-1$ 行，每行两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \ne v$），表示 $T$ 中的一条边。保证这些边构成一棵树。 接下来 $q$ 行，每行两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \ne v$），表示要添加或删除的边的两个端点。保证这些边不属于 $T$。

对于每次操作，输出一个整数 $k$，表示当前图中“好”顶点的数量。

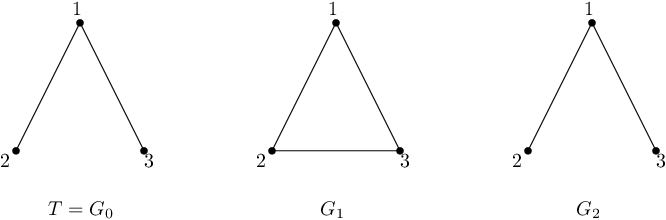
第一个样例如下图所示：  第一次操作后，$G$ 包含所有三条可能的边。DFS 的结果如下： - 若起点为 $1$，有两种邻居遍历顺序，分别为 $[2, 3]$ 或 $[3, 2]$。 - 若选择前者，则先访问 $2$，无论后续如何，下一步都会访问 $3$，生成树包含边 $\{1,2\}$ 和 $\{2,3\}$，不等于 $T$。 - 若选择后者，生成树包含边 $\{1,3\}$ 和 $\{2,3\}$。 因此，无论如何排序，都无法使 DFS 生成 $T$，所以 $1$ 不是“好”顶点。 - 若起点为 $2$，有两种遍历顺序。若先访问 $3$，生成树为 $\{2,3\}$ 和 $\{1,3\}$，不等于 $T$。若先访问 $1$，只能继续访问 $3$，生成树为 $\{1,2\}$ 和 $\{1,3\}$，等于 $T$，所以 $2$ 是“好”顶点。 - 起点为 $3$ 的情况与 $2$ 对称，因此 $3$ 也是“好”顶点。 所以答案为 $2$。第二次操作后，$2$ 和 $3$ 之间的边被删除，$G = T$，无论起点如何，DFS 生成树都等于 $T$，所以答案为 $3$。 第二个样例中，每次操作后的“好”顶点集合分别为： - $\{2, 3, 5\}$ - $\{3, 5\}$ - $\{3, 4, 5\}$ - $\{4, 5\}$ - $\{4, 5, 6\}$ - $\{5, 6\}$ 由 ChatGPT 4.1 翻译