CF1046I Say Hello

两个朋友正在芭比星系旅行。如果他们的距离小于或等于 $d _ 1$，并且这是他们第一次交谈或者在他们上次互相打招呼后的某个时间点，他们的距离大于 $d_2$，那么他们会互相打一次招呼。 我们需要计算这两位朋友打招呼的次数。有 $n$ 个时刻，对于每个人，我们知道他在每个时刻的位置。位置都是在二维平面上的整点。 一个人可以在两个时刻之间保持相同的位置，但是如果一个人在两个时刻之间的位置不同，我们假设他会以恒定的速度在恒定的方向上从上个时刻移动到下个时刻。

第一行一个正整数 $n \ (2 \le n \le 10 ^ 5)$。 接下来一行两个正整数 $d _ 1, d _ 2\ (0 < d _ 1 < d _ 2 < 1000)$。 随后 $n$ 行，每行四个整数 $A _ x, A _ y, B _ x, B _ y\ (0 \le A _ x, A _ y, B _ x, B _ y \le 1000)$ 表示两个人 $A, B$ 在该时刻的位置。

输出包含一个整数，表示朋友彼此之间打招呼的次数。

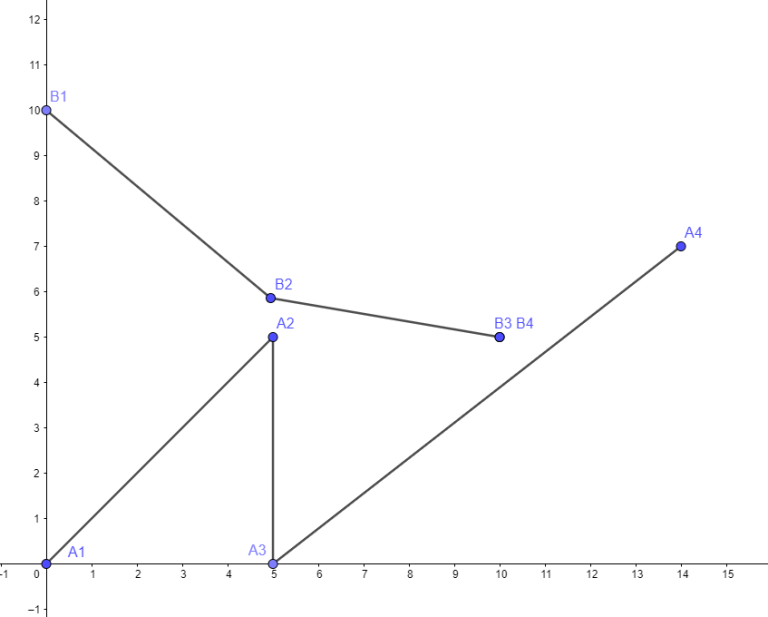 Explanation: Friends should send signals 2 times to each other, first time around point $ A2 $ and $ B2 $ and second time during A's travel from point $ A3 $ to $ A4 $ while B stays in point $ B3=B4 $ .