CF1054F Electric Scheme
题目描述
Pasha 是一名年轻的技术员,尽管如此,他已经有了一个宏伟的目标:组装一台电脑。他需要熟悉的第一个任务就是组装一套电路图。
Pasha 昨天组装的电路图由若干根导线组成。每根导线是连接平面上两个整点坐标的线段,且坐标范围在 $[1, 10^9]$ 内。
电路图中有两种颜色的导线:
- 红色导线:这些导线是水平线段,即如果一根红色导线连接两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$,那么 $y_1 = y_2$;
- 蓝色导线:这些导线是竖直线段,即如果一根蓝色导线连接两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$,那么 $x_1 = x_2$。
注意,如果一根导线连接的是同一个点,它既可以是红色,也可以是蓝色。同时,在 Pasha 的电路图中,同色的两根导线不会相交,即不存在两根同色导线有公共点。
Pasha 的电路图有个缺陷:导线没有绝缘,所以在两种不同颜色导线相交的点上,Pasha 看到火花。Pasha 记录下了所有看到火花的点,得到了 $n$ 个不同的点。之后他拆除了电路图。
第二天早上,Pasha 看着这 $n$ 个看到火花的点,想知道他到底用了多少根导线。不幸的是,他已经记不清了,所以他现在想知道,他最少可能用了多少根导线。请你帮他确定这个最小数量,并给出一种导线的布置方式,使得最终电路图中火花出现的位置与输入完全一致。
输入格式
第一行包含一个整数 $n$($1 \leq n \leq 1000$),表示 Pasha 看到火花的点的数量。
接下来的 $n$ 行,每行包含两个整数 $x$ 和 $y$($1 \leq x, y \leq 10^9$),表示一个有火花的点的坐标。保证所有点两两不同。
输出格式
输出电路图的描述,格式如下:
第一行输出 $h$,表示水平红色导线的数量($0 \leq h$)。接下来的 $h$ 行,每行输出 $4$ 个整数 $x_1, y_1, x_2, y_2$,表示一根红色导线连接的两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$。这些线段必须是水平的,即 $y_1 = y_2$。同时需满足 $1 \leq x_1, y_1, x_2, y_2 \leq 10^9$。
然后输出 $v$,表示竖直蓝色导线的数量($0 \leq v$)。接下来的 $v$ 行,每行输出 $4$ 个整数 $x_1, y_1, x_2, y_2$,表示一根蓝色导线连接的两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$。这些线段必须是竖直的,即 $x_1 = x_2$。同时需满足 $1 \leq x_1, y_1, x_2, y_2 \leq 10^9$。
同色的两根线段不能有公共点。火花出现的点集必须与输入完全一致。
线段总数 $h + v$ 必须尽量少。可以证明一定存在解。如果有多种方案,输出任意一种均可。
说明/提示
在第一个样例中,Pasha 可以组装如下的电路图:
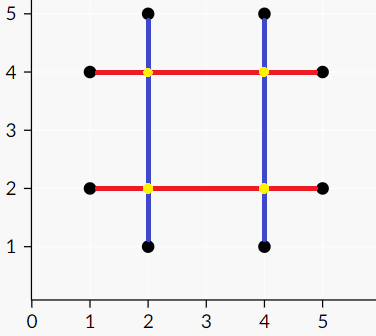
在这个电路图中,有 $2$ 根红色导线,分别连接 $(5, 2)$ 与 $(1, 2)$,以及 $(1, 4)$ 与 $(5, 4)$;有 $2$ 根蓝色导线,分别连接 $(2, 1)$ 与 $(2, 5)$,以及 $(4, 5)$ 与 $(4, 1)$。注意,火花只会出现在输入描述的那些点,在图中用黄色标出。例如,Pasha 会在 $(2, 4)$ 看到火花,因为第二根红色导线和第一根蓝色导线在此相交。可以证明,无法用少于 $4$ 根导线实现相同的火花分布。
由 ChatGPT 4.1 翻译