CF1055F Tree and XOR
题目描述
给定一棵包含 $n$ 个顶点的无环连通无向图(即一棵树),树的每条边上都写有一个非负整数。
对于所有顶点对 $(v, u)$(一共恰好有 $n^2$ 个),对于每一对,计算从 $v$ 到 $u$ 的简单路径上所有边权的按位异或(xor)值。如果路径只包含一个顶点,则该路径上所有边权的异或值为 $0$。
假设将所有得到的 $n^2$ 个值按非降序排列。你需要找出其中第 $k$ 小的值。
异或的定义如下:
给定两个整数 $x$ 和 $y$,考虑它们的二进制表示(可能有前导零):$x_k \dots x_2 x_1 x_0$ 和 $y_k \dots y_2 y_1 y_0$(其中 $k$ 足够大以容纳 $x$ 和 $y$ 的所有位)。这里 $x_i$ 表示 $x$ 的第 $i$ 位,$y_i$ 表示 $y$ 的第 $i$ 位。令 $r = x \oplus y$ 表示 $x$ 和 $y$ 的异或操作结果。那么 $r$ 的定义为 $r_k \dots r_2 r_1 r_0$,其中:
$$
r_i = \left\{
\begin{aligned}
1, ~ \text{如果} ~ x_i \ne y_i \\
0, ~ \text{如果} ~ x_i = y_i
\end{aligned}
\right.
$$
输入格式
第一行包含两个整数 $n$ 和 $k$($2 \le n \le 10^6$,$1 \le k \le n^2$),分别表示树的顶点数和按非降序排列后第 $k$ 小的路径异或值。
接下来的 $n-1$ 行,每行包含两个整数 $p_i$ 和 $w_i$($1 \le p_i \le i$,$0 \le w_i < 2^{62}$),分别表示顶点 $i+1$ 的父节点编号和该边的权值。
输出格式
输出一个整数,表示第 $k$ 小的路径异或值。
说明/提示
第二个样例的树结构如下:
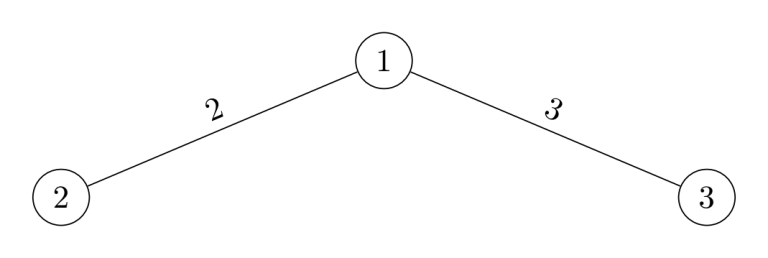
对于这样的树,一共有 $9$ 条路径:
1. $1 \to 1$,值为 $0$
2. $2 \to 2$,值为 $0$
3. $3 \to 3$,值为 $0$
4. $2 \to 3$(经过 $1$),值为 $1 = 2 \oplus 3$
5. $3 \to 2$(经过 $1$),值为 $1 = 2 \oplus 3$
6. $1 \to 2$,值为 $2$
7. $2 \to 1$,值为 $2$
8. $1 \to 3$,值为 $3$
9. $3 \to 1$,值为 $3$
由 ChatGPT 4.1 翻译