CF1060C Maximum Subrectangle

给定两个正整数数组 $a$ 和 $b$，长度分别为 $n$ 和 $m$。 定义 $c$ 为一个 $n \times m$ 的矩阵，其中 $c_{i,j} = a_i \cdot b_j$。 你需要在矩阵 $c$ 中找到一个子矩形，使得其所有元素之和不超过 $x$，并且其面积（即包含的元素个数）尽可能大。 形式化地，你需要找到最大的整数 $s$，使得存在整数 $x_1, x_2, y_1, y_2$，满足 $1 \leq x_1 \leq x_2 \leq n$，$1 \leq y_1 \leq y_2 \leq m$，$(x_2 - x_1 + 1) \times (y_2 - y_1 + 1) = s$，且 $\sum_{i=x_1}^{x_2} \sum_{j=y_1}^{y_2} c_{i,j} \leq x$。

第一行包含两个整数 $n$ 和 $m$（$1 \leq n, m \leq 2000$）。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \leq a_i \leq 2000$）。 第三行包含 $m$ 个整数 $b_1, b_2, \ldots, b_m$（$1 \leq b_j \leq 2000$）。 第四行包含一个整数 $x$（$1 \leq x \leq 2 \times 10^9$）。

如果存在四个整数 $x_1, x_2, y_1, y_2$，满足 $1 \leq x_1 \leq x_2 \leq n$，$1 \leq y_1 \leq y_2 \leq m$，且 $\sum_{i=x_1}^{x_2} \sum_{j=y_1}^{y_2} c_{i,j} \leq x$，则输出所有满足条件的四元组中 $(x_2 - x_1 + 1) \times (y_2 - y_1 + 1)$ 的最大值，否则输出 $0$。

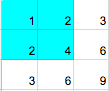
以下为第一个样例的矩阵及选中的子矩形（蓝色部分）：  以下为第二个样例的矩阵及选中的子矩形（蓝色部分）：  由 ChatGPT 4.1 翻译