CF1060C Maximum Subrectangle

You are given two arrays $ a $ and $ b $ of positive integers, with length $ n $ and $ m $ respectively. Let $ c $ be an $ n \times m $ matrix, where $ c_{i,j} = a_i \cdot b_j $ . You need to find a subrectangle of the matrix $ c $ such that the sum of its elements is at most $ x $ , and its area (the total number of elements) is the largest possible. Formally, you need to find the largest number $ s $ such that it is possible to choose integers $ x_1, x_2, y_1, y_2 $ subject to $ 1 \leq x_1 \leq x_2 \leq n $ , $ 1 \leq y_1 \leq y_2 \leq m $ , $ (x_2 - x_1 + 1) \times (y_2 - y_1 + 1) = s $ , and $ \sum_{i=x_1}^{x_2}{\sum_{j=y_1}^{y_2}{c_{i,j}}} \leq x. $

The first line contains two integers $ n $ and $ m $ ( $ 1 \leq n, m \leq 2000 $ ). The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \leq a_i \leq 2000 $ ). The third line contains $ m $ integers $ b_1, b_2, \ldots, b_m $ ( $ 1 \leq b_i \leq 2000 $ ). The fourth line contains a single integer $ x $ ( $ 1 \leq x \leq 2 \cdot 10^{9} $ ).

If it is possible to choose four integers $ x_1, x_2, y_1, y_2 $ such that $ 1 \leq x_1 \leq x_2 \leq n $ , $ 1 \leq y_1 \leq y_2 \leq m $ , and $ \sum_{i=x_1}^{x_2}{\sum_{j=y_1}^{y_2}{c_{i,j}}} \leq x $ , output the largest value of $ (x_2 - x_1 + 1) \times (y_2 - y_1 + 1) $ among all such quadruplets, otherwise output $ 0 $ .

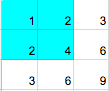
Matrix from the first sample and the chosen subrectangle (of blue color):  Matrix from the second sample and the chosen subrectangle (of blue color):