CF1062F Upgrading Cities

在 $X$ 王国中有 $n$ 个城市，编号从 $1$ 到 $n$。人们通过一些单向道路在城市之间旅行。作为一名乘客，JATC 觉得很奇怪，因为从任意城市 $u$ 出发，他都无法通过王国的道路回到该城市。也就是说，这个王国的道路系统可以看作是一张有向无环图。 JATC 对这种出行系统感到不满，决定去见国王并请求他做出改变。国王回应说，他会升级一些城市以方便出行。但由于预算有限，国王只会升级那些“重要”或“半重要”的城市。对于一个城市 $u$，如果对于任意城市 $v \neq u$，要么存在从 $u$ 到 $v$ 的路径，要么存在从 $v$ 到 $u$ 的路径，则称 $u$ 为重要城市。如果 $u$ 不是重要城市，但可以通过摧毁恰好一个城市 $v \neq u$ 使得 $u$ 变为重要城市，则称 $u$ 为半重要城市。 一旦国王找出所有这样的城市，他就会立即采取行动。请你帮助国王加快这个过程。

输入的第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 300\,000$，$1 \le m \le 300\,000$），分别表示城市数量和单向道路数量。 接下来的 $m$ 行描述了王国的道路系统。每行包含两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$，$u_i \neq v_i$），表示一条从 $u_i$ 到 $v_i$ 的单向道路。 保证王国的道路系统是一张有向无环图，不存在重边和自环。

输出一个整数，表示国王需要升级的城市数量。

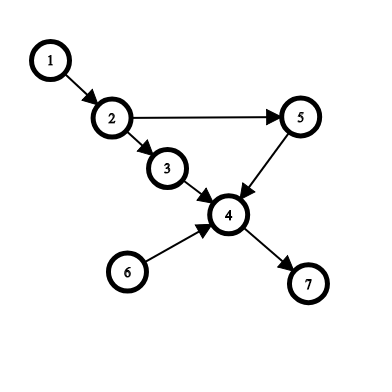
在第一个样例中：  - 从城市 $1$ 出发可以到达除城市 $6$ 外的所有城市，同时从城市 $6$ 也无法到达城市 $1$。因此，如果摧毁城市 $6$，城市 $1$ 就会变为重要城市，所以 $1$ 是半重要城市。 - 对于城市 $2$，无法到达且无法被到达的城市集合为 $\{6\}$。因此，摧毁城市 $6$ 会使城市 $2$ 变为重要城市，所以 $2$ 也是半重要城市。 - 对于城市 $3$，该集合为 $\{5, 6\}$。可以看到，无论摧毁城市 $5$ 还是 $6$，都无法使城市 $3$ 变为重要城市，因此 $3$ 既不是重要城市也不是半重要城市。 - 对于城市 $4$，该集合为空集，所以 $4$ 是重要城市。 - 城市 $5$ 的集合为 $\{3, 6\}$，城市 $6$ 的集合为 $\{3, 5\}$，同理，这两个城市都不是重要城市也不是半重要城市。 - 城市 $7$ 是重要城市，因为所有其他城市都能到达它。 所以有两个重要城市（$4$ 和 $7$）和两个半重要城市（$1$ 和 $2$）。 在第二个样例中，重要城市是 $1$ 和 $4$，半重要城市是 $2$ 和 $3$。 由 ChatGPT 4.1 翻译