CF1065F Up and Down the Tree
题目描述
你有一棵带有 $n$ 个结点的树,根是结点 $1$。有一个标记,最初在根结点处。你可以将标记移动到其他结点处。假设标记当前所在结点为 $v$,你可以做出以下两种操作:
1. 将标记移动到 $v$ 子树的任一叶子处。
2. 如果是结点 $v$ 为叶子,则将标记向根移动不超过 $k$ 次。换句话说,如果 $h_v$ 为结点 $v$ 的深度 (根的深度为 $0$),你可以将其移动到顶点 $to$($to$ 为 $v$ 祖先)并且 $h_v-k\le h_{to}$。
根不是叶子(即使它的度数是 $1$)。计算最多能访问多少叶子。
输入格式
- 第一行包含两个整数 $n$ 和 $k(1\le k
输出格式
输出一个整数,表示可以访问的最大叶子数。
说明/提示
The graph from the first example:
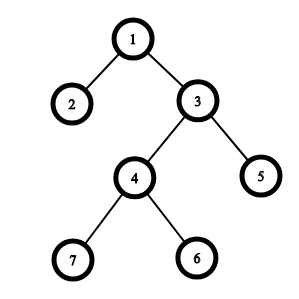One of the optimal ways is the next one: $ 1 \rightarrow 2 \rightarrow 1 \rightarrow 5 \rightarrow 3 \rightarrow 7 \rightarrow 4 \rightarrow 6 $ .
The graph from the second example:
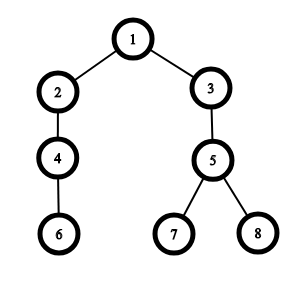One of the optimal ways is the next one: $ 1 \rightarrow 7 \rightarrow 5 \rightarrow 8 $ . Note that there is no way to move from $ 6 $ to $ 7 $ or $ 8 $ and vice versa.