CF1066F Yet another 2D Walking

Maksim 在笛卡尔平面上行走。最初，他站在点 $(0, 0)$，每一步他可以移动到四个相邻的点之一（左、右、上、下）。例如，如果 Maksim 当前在点 $(0, 0)$，他可以在一步内移动到以下任意一个点： - $(1, 0)$； - $(0, 1)$； - $(-1, 0)$； - $(0, -1)$。 在平面上还有 $n$ 个不同的关键点。第 $i$ 个关键点为 $p_i = (x_i, y_i)$。保证 $0 \le x_i$ 且 $0 \le y_i$，且没有关键点为 $(0, 0)$。 定义第 $k$ 层的点为满足 $max(x_i, y_i) = k$ 的点。例如，第一层的点满足 $max(x_i, y_i) = 1$，第二层的点满足 $max(x_i, y_i) = 2$，以此类推。Maksim 想要访问所有关键点。但他不能在未访问完第 $i$ 层的所有点之前访问第 $i+1$ 层的点。他从给定关键点集合中最小层级的点开始访问。 两点 $(x_1, y_1)$ 和 $(x_2, y_2)$ 之间的距离为 $|x_1 - x_2| + |y_1 - y_2|$，其中 $|v|$ 表示 $v$ 的绝对值。 Maksim 想以总路程最小的方式访问所有关键点。你的任务是求出他需要行走的最小总距离。 如果你使用 Python 编程，建议提交时使用 PyPy 以获得更好的性能。

输入的第一行包含一个整数 $n$（$1 \le n \le 2 \times 10^5$），表示关键点的数量。 接下来的 $n$ 行，每行包含两个整数 $x_i, y_i$（$0 \le x_i, y_i \le 10^9$），表示第 $i$ 个关键点 $p_i$ 的 $x$ 坐标和 $y$ 坐标。保证所有点互不相同，且没有点为 $(0, 0)$。

输出一个整数，表示 Maksim 按照上述规则访问所有关键点所需行走的最小总距离。

第一个样例对应的图示如下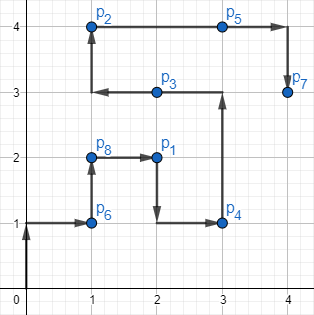： 其中一种长度为 $15$ 的可行方案。 第二个样例对应的图示如下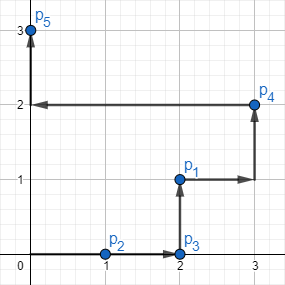： 其中一种长度为 $9$ 的可行方案。 由 ChatGPT 4.1 翻译