CF1067B Multihedgehog

有人送给 Ivan 一个奇怪的生日礼物。这是一只“刺猬”——一个连通无向图，其中有一个顶点的度数至少为 $3$（我们称之为中心），其余所有顶点的度数均为 $1$。Ivan 觉得刺猬太无聊了，于是决定自己制作 $k$-多重刺猬。 我们定义 $k$-多重刺猬如下： - $1$-多重刺猬就是刺猬：它有一个度数至少为 $3$ 的顶点，以及若干度数为 $1$ 的顶点。 - 对于所有 $k \ge 2$，$k$-多重刺猬是在 $(k-1)$-多重刺猬的基础上，对每个度数为 $1$ 的顶点 $v$ 进行如下操作：设 $u$ 为其唯一的邻居；删除顶点 $v$，新建一个以顶点 $w$ 为中心的刺猬，并用一条边连接 $u$ 和 $w$。新建的每个刺猬可以彼此不同，也可以与最初的刺猬不同。 因此，$k$-多重刺猬一定是一棵树。Ivan 制作了 $k$-多重刺猬，但他不确定自己是否没有出错。因此他请你帮忙判断，他制作的树是否真的是 $k$-多重刺猬。

输入的第一行包含两个整数 $n$、$k$（$1 \le n \le 10^{5}$，$1 \le k \le 10^{9}$），分别表示顶点数和刺猬参数。 接下来的 $n-1$ 行，每行包含两个整数 $u$、$v$（$1 \le u,\, v \le n;\, u \ne v$），表示一条连接顶点 $u$ 和 $v$ 的边。 保证给定的图是一棵树。

如果给定的树是 $k$-多重刺猬，输出 "Yes"（不含引号）；否则输出 "No"（不含引号）。

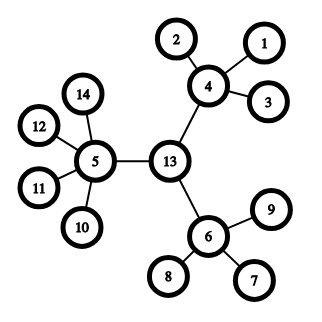
第一个样例中的 $2$-多重刺猬如下图所示：  其中心为顶点 $13$。最后一步新建的刺猬分别为：\ [4（中心），1，2，3\]，\ [6（中心），7，8，9\]，\ [5（中心），10，11，12，13\]。 第二个样例中的树不是刺猬，因为中心的度数应至少为 $3$。 由 ChatGPT 4.1 翻译