CF1067C Knights

Ivan 在无限大的国际象棋棋盘上放置骑士。最初棋盘上有 $n$ 个骑士。如果存在一个空格子被至少 $4$ 个骑士攻击到，那么他就在这个格子上放置一个新的骑士。Ivan 重复这个过程，直到不存在这样的空格子为止。可以证明，这个过程是有限的。也可以证明，最终的棋子分布与新骑士放置的顺序无关。 Ivan 让你找到一种恰好放置 $n$ 个骑士的初始方案，使得最终棋盘上至少有 $\lfloor \frac{n^{2}}{10} \rfloor$ 个骑士。

输入仅一行，包含一个整数 $n$（$1 \le n \le 10^{3}$），表示初始放置的骑士数量。

输出 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$-10^{9} \le x_i,\, y_i \le 10^{9}$），表示第 $i$ 个骑士的坐标。对于所有 $i \ne j$，$(x_i,\, y_i) \ne (x_j,\, y_j)$，即所有骑士必须放在不同的格子上。 保证一定存在解。

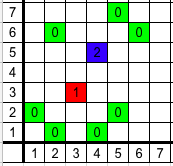
让我们来看第二个样例：  绿色的 0 表示初始放置的骑士。格子 $(3,\, 3)$ 被 $(1,\, 2)$、$(2,\, 1)$、$(4,\, 1)$ 和 $(5,\, 2)$ 这四个格子的骑士攻击，因此 Ivan 会在这个格子放置一个新的骑士。格子 $(4,\, 5)$ 最初只被 $(2,\, 6)$、$(5,\, 7)$ 和 $(6,\, 6)$ 这三个骑士攻击。但新放置在 $(3,\, 3)$ 的骑士也会攻击 $(4,\, 5)$，此时它被 $4$ 个骑士攻击，Ivan 会在这个格子再放一个骑士。此时没有更多被 $4$ 个或更多骑士攻击的空格子，过程结束。最终棋盘上有 $9$ 个骑士，不小于 $\lfloor \frac{7^{2}}{10} \rfloor = 4$。 由 ChatGPT 4.1 翻译