CF1068C Colored Rooks

Ivan 是一名新手画家。他有 $n$ 种不同颜色的染料。他还确切地知道 $m$ 对能够和谐搭配的颜色对。 Ivan 还喜欢下国际象棋。他有 $5000$ 个车。他想取出 $k$ 个车，将每个车涂成 $n$ 种颜色中的一种，然后把这 $k$ 个车放在一个 $10^{9} \times 10^{9}$ 的棋盘上。 我们称棋盘上的一组车是连通的，如果从任意一个车出发，只通过这组车所在的格子，可以到达这组中的任意其他车。假设车可以“跳过”其他车，也就是说，一个车可以移动到任意与其同行或同列的格子。 Ivan 希望他的车的摆放满足以下条件： - 对于每种颜色，棋盘上至少有一个这种颜色的车； - 对于每种颜色，这种颜色的所有车组成的集合是连通的； - 对于任意两种不同颜色 $a$ 和 $b$，如果且仅如果这两种颜色能够和谐搭配，则颜色 $a$ 和颜色 $b$ 的所有车的集合的并集是连通的。 请你帮助 Ivan 找到一种满足条件的车的摆放方案。

输入的第一行包含两个整数 $n$ 和 $m$（$1 \le n \le 100$，$0 \le m \le \min(1000,\,\, \frac{n(n-1)}{2})$）——颜色的数量以及能够和谐搭配的颜色对的数量。 接下来的 $m$ 行，每行给出一对能够和谐搭配的颜色。颜色编号为 $1$ 到 $n$。保证没有重复的颜色对。

输出 $n$ 个区块，第 $i$ 个区块描述第 $i$ 种颜色的车。 每个区块的第一行输出一个整数 $a_i$（$1 \le a_i \le 5000$）——第 $i$ 种颜色的车的数量。接下来的 $a_i$ 行，每行输出两个整数 $x$ 和 $y$（$1 \le x,\,\, y \le 10^{9}$）——该颜色的一个车的坐标。 所有车必须放在不同的格子上。 所有车的总数不得超过 $5000$。 保证一定存在解。

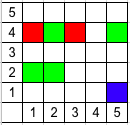
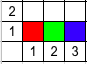
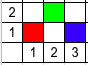
下图展示了所有三个样例的车的摆放方式（红色为颜色 $1$，绿色为颜色 $2$，蓝色为颜色 $3$）。    由 ChatGPT 4.1 翻译