CF1071E Rain Protection

许多人都梦想拥有敞篷车（也常被称为 cabriolet）。然而，有些敞篷车根本没有车顶，因此容易被雨淋。正因如此，著名发明家 Melon Ask 决定为敞篷车设计一种防雨机制。 该机制的工作区域是驾驶员正上方的一个平面区域。其功能部分由两条滑轨组成，滑轨上有一根可伸缩绳索的两个端点。为简化问题，我们可以将其视为平面上的两条平行线段，以及一条连接这两条线段的绳索段，绳索的两个端点可以自由选择在线段上的任意位置。 算法部分能够检测每一滴雨，并预测其何时、何地落到平面上。恰好在这一时刻，绳索段必须覆盖该雨滴落点（即绳索吸收雨滴）。 现给定绳索端点的初始位置以及所有雨滴的信息。你需要选择端点滑动的最小可能速度 $v$（两个端点可以各自独立地沿各自的线段任意方向滑动），使得可以通过移动端点（速度不超过 $v$）捕捉到所有雨滴，或者判断无论速度多大都无法做到。

第一行包含三个整数 $n$、$w$ 和 $h$（$1 \le n \le 10^5$，$1 \le w, h \le 10^3$），表示有 $n$ 个雨滴，两条滑轨分别为连接 $(0, 0)$ 与 $(w, 0)$ 以及连接 $(0, h)$ 与 $(w, h)$ 的线段。 第二行包含两个整数 $e_1$ 和 $e_2$，表示初始时刻（即 $t = 0$）绳索端点的位置分别为 $(e_1, 0)$ 和 $(e_2, h)$（$0 \le e_1, e_2 \le w$）。 接下来的 $n$ 行中，第 $i$ 行包含三个整数 $t_i$、$x_i$ 和 $y_i$（$1 \le t_i \le 10^5$，$0 \le x_i \le w$，$0 < y_i < h$），表示第 $i$ 个雨滴在时刻 $t_i$ 落在点 $(x_i, y_i)$。保证 $t_i \le t_{i+1}$ 对所有合法的 $i$ 成立。

如果无法捕捉到所有雨滴，输出 $-1$。 否则，输出能够捕捉所有雨滴的最小最大速度。若你的答案与标准答案的绝对或相对误差不超过 $10^{-4}$，则视为正确。 形式化地，设你的答案为 $a$，标准答案为 $b$，若 $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}$，则你的答案被认为是正确的。

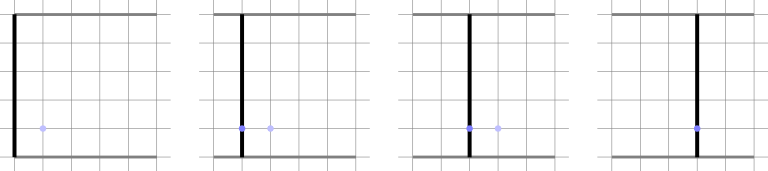
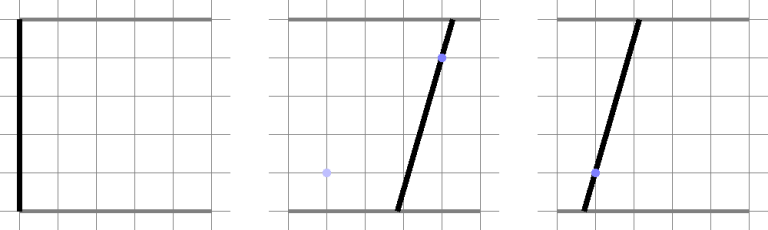
以下是第一个样例的操作示意图：  第二个样例的操作示意图如下：  由 ChatGPT 4.1 翻译