CF1075A The King's Race
题目描述
在一个宽为 $n$、高为 $n$ 的国际象棋棋盘上,行号从下到上依次为 $1$ 到 $n$,列号从左到右依次为 $1$ 到 $n$。因此,棋盘上的每一个格子都可以用坐标 $(r, c)$ 表示,其中 $r$ 表示行号,$c$ 表示列号。
白王已经在坐标为 $(1,1)$ 的格子上坐了一千年,而黑王则一直坐在坐标为 $(n,n)$ 的格子上。他们本可以继续这样坐下去,但突然有一枚漂亮的硬币掉在了坐标为 $(x, y)$ 的格子上……
两位国王都想得到这枚硬币,于是他们决定按照稍作修改的国际象棋规则来进行一场竞赛:
与国际象棋一样,白王先走一步,黑王再走一步,接着白王再走一步,如此交替进行。然而,在本题中,两个国王可以同时站在相邻的格子,甚至可以同时站在同一个格子。
谁先到达硬币所在的格子 $(x, y)$,谁就获胜。
我们回顾一下,国王是一种可以向所有方向移动一格的棋子,也就是说,如果国王当前在 $(a, b)$,那么他可以一步移动到 $(a+1, b)$、$(a-1, b)$、$(a, b+1)$、$(a, b-1)$、$(a+1, b-1)$、$(a+1, b+1)$、$(a-1, b-1)$ 或 $(a-1, b+1)$。禁止走出棋盘之外。
请判断,如果白王先走,谁会先到达 $(x, y)$ 所在的格子。
输入格式
第一行包含一个整数 $n$($2 \le n \le 10^{18}$),表示棋盘的边长。
第二行包含两个整数 $x$ 和 $y$($1 \le x, y \le n$),表示硬币掉落的格子的坐标。
输出格式
输出一行,如果白王会获胜,则输出 "White"(不带引号);如果黑王会获胜,则输出 "Black"(不带引号)。
你可以用任意大小写输出答案。
说明/提示
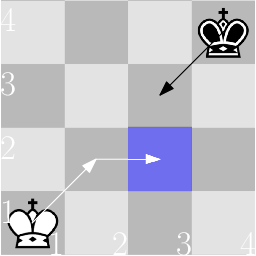
下面是第一个样例的竞赛过程示例,假设两位国王都采取最优策略:
1. 白王从 $(1,1)$ 移动到 $(2,2)$。
2. 黑王从 $(4,4)$ 移动到 $(3,3)$。
3. 白王从 $(2,2)$ 移动到 $(2,3)$,这就是硬币所在的格子,因此白王获胜。
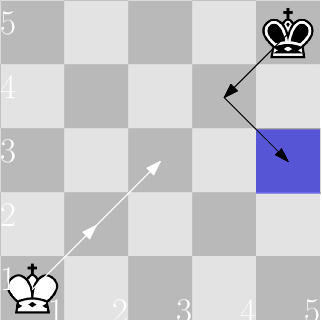
下面是第二个样例的竞赛过程示例,假设两位国王都采取最优策略:
1. 白王从 $(1,1)$ 移动到 $(2,2)$。
2. 黑王从 $(5,5)$ 移动到 $(4,4)$。
3. 白王从 $(2,2)$ 移动到 $(3,3)$。
4. 黑王从 $(4,4)$ 移动到 $(3,5)$,这就是硬币所在的格子,因此黑王获胜。
在第三个样例中,硬币正好掉在了黑王的起始格子,因此黑王立即获胜。

由 ChatGPT 4.1 翻译