CF1082D Maximum Diameter Graph

图的构造性问题又来了！这一次，你需要构造的图需要满足以下性质。 如果任意一对顶点之间都存在一条路径，则称该图是连通的。 一个连通无向图的直径（即“最长的最短路”）是任意一对顶点之间最短路径中边数的最大值。 一个顶点的度是与其相连的边的数量。 给定一个长度为 $n$ 的整数序列 $a_1, a_2, \dots, a_n$，请你构造一个有 $n$ 个顶点的连通无向图，使得： - 图中不包含自环和重边； - 第 $i$ 个顶点的度 $d_i$ 不超过 $a_i$（即 $d_i \le a_i$）； - 图的直径尽可能大。 请输出构造出的图，或者报告无解。

第一行包含一个整数 $n$（$3 \le n \le 500$），表示图中顶点的数量。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$（$1 \le a_i \le n-1$），表示每个顶点度数的上限。

如果不存在满足条件的图，输出 “NO”。 否则，第一行输出 “YES” 和所构造图的直径。 第二行输出一个整数 $m$，表示图中的边数。 接下来的 $m$ 行，每行输出两个整数 $v_i, u_i$（$1 \le v_i, u_i \le n$，$v_i \neq u_i$），表示一条边的两个端点。图中不应有重边——对于每一对 $(x, y)$，你只应输出一次 $(x, y)$ 或 $(y, x)$。

以下是前两个样例的图示。两者的直径均为 $2$。 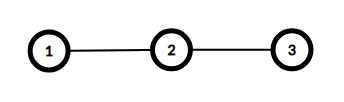 $d_1 = 1 \le a_1 = 2$，$d_2 = 2 \le a_2 = 2$，$d_3 = 1 \le a_3 = 2$ 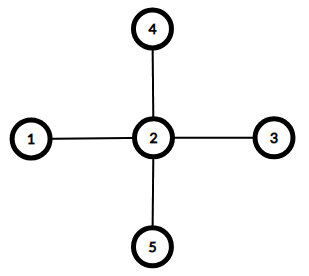 $d_1 = 1 \le a_1 = 1$，$d_2 = 4 \le a_2 = 4$，$d_3 = 1 \le a_3 = 1$，$d_4 = 1 \le a_4 = 1$ 由 ChatGPT 4.1 翻译