CF1083A The Fair Nut and the Best Path

Fair Nut 准备前往 Tree Country 旅行，这个国家有 $n$ 个城市。该国大部分土地被森林覆盖。此外，当地的公路系统构成了一棵树（即一个无环连通图）。Nut 想在城市 $u$ 租一辆车，并沿一条简单路径前往城市 $v$。他尚未决定具体路径，现在正是选择的时候。注意，所选路径可以只包含一个顶点。 每个城市都有一个加油站。由于奇怪的法律，Nut 在第 $i$ 个城市最多只能购买 $w_i$ 升汽油。可以假设他有无限的钱。每条道路都有一定长度，当 Nut 驾车通过这条道路时，汽油量会减少相应的长度。当然，Nut 不能选择一条会导致汽油耗尽的路径。他可以在每个经过的城市加油，包括起点和终点。 他还想知道，在路径终点他最多能剩下多少汽油。请你帮他计算这个最大值。

第一行包含一个整数 $n$（$1 \leq n \leq 3 \cdot 10^5$），表示城市数量。 第二行包含 $n$ 个整数 $w_1, w_2, \ldots, w_n$（$0 \leq w_i \leq 10^9$），表示 Nut 在每个城市最多能购买的汽油量。 接下来的 $n-1$ 行，每行包含三个整数 $u, v, c$（$1 \leq u, v \leq n$，$1 \leq c \leq 10^9$，$u \ne v$），表示城市 $u$ 和 $v$ 之间有一条长度为 $c$ 的道路。 保证道路连通性图是一棵树。

输出一个整数，表示他在路径终点最多能剩下的汽油量。

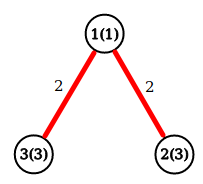
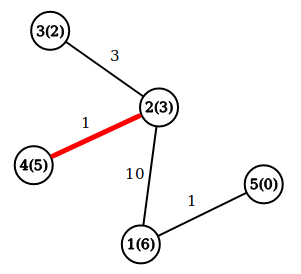
第一个样例的最优路径是 $2 \to 1 \to 3$。  第二个样例的最优路径是 $2 \to 4$。  由 ChatGPT 4.1 翻译