CF1083C Max Mex

Grisha 发现了一棵以节点 $1$ 为根的树（即一个无环连通图）。 但这棵树并不是普通的树。每个节点上都写有一个从 $0$ 到 $n-1$ 的排列 $p$，即在节点 $i$ 上写有数字 $p_i$。 Grisha 喜欢为自己发明一些奇怪又有趣的问题，但他并不总能解决这些问题，所以你需要帮助他处理关于这棵树的两种操作。 我们定义函数 $MEX(S)$，其中 $S$ 是一个非负整数集合，$MEX(S)$ 表示不在 $S$ 中的最小非负整数。 设 $l$ 是树上的一条简单路径。记路径上节点的编号为 $u_1, u_2, \ldots, u_k$。 定义 $V(l)$ 为集合 $\{p_{u_1}, p_{u_2}, \ldots, p_{u_k}\}$。 操作有两种： 1. 对于两个节点 $i$ 和 $j$，交换 $p_i$ 和 $p_j$ 的值。 2. 在所有可能的路径 $l$ 中，求 $MEX(V(l))$ 的最大值。

第一行包含一个整数 $n$（$2 \leq n \leq 2 \cdot 10^5$），表示树的节点数。 第二行包含 $n$ 个整数，分别为 $p_1, p_2, \ldots, p_n$（$0 \leq p_i < n$），即排列 $p$，保证所有数字互不相同。 第三行包含 $n-1$ 个整数，分别为 $d_2, d_3, \ldots, d_n$（$1 \leq d_i < i$），其中 $d_i$ 表示节点 $i$ 在树中的直接父节点。 第四行包含一个整数 $q$（$1 \leq q \leq 2 \cdot 10^5$），表示操作的数量。 接下来的 $q$ 行，每行描述一个操作： 每行开头有一个整数 $t$（$1$ 或 $2$），表示操作类型： 1. 如果 $t=1$，该行还包含两个整数 $i$ 和 $j$（$1 \leq i, j \leq n$），表示需要交换排列中节点 $i$ 和节点 $j$ 的值。 2. 如果 $t=2$，则需要在所有路径 $l$ 中，求 $MEX(V(l))$ 的最大值。

对于每个类型为 $2$ 的操作，输出一个整数，表示该操作的答案。

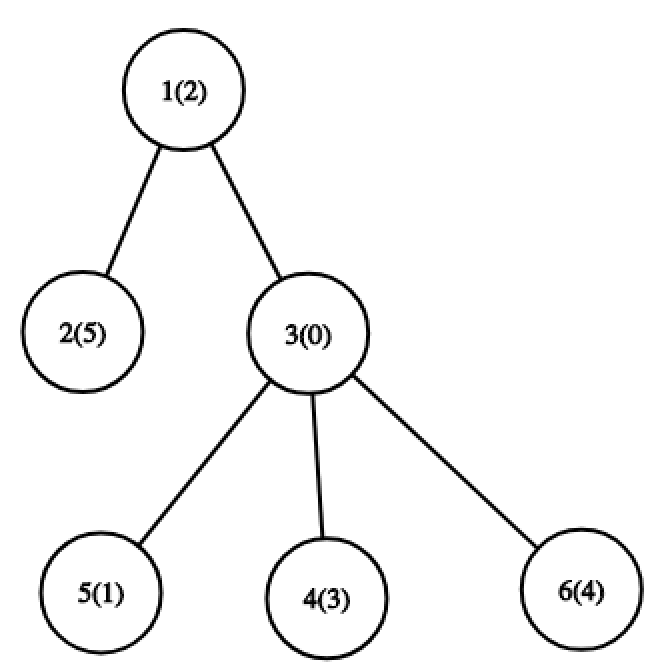
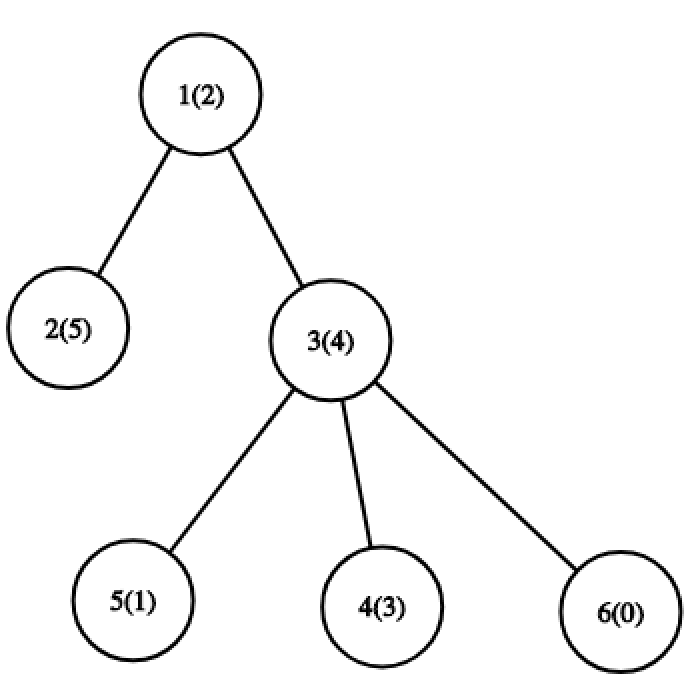
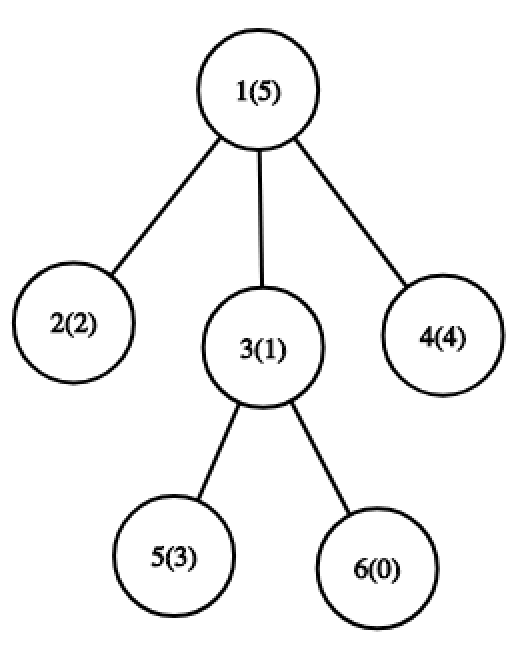
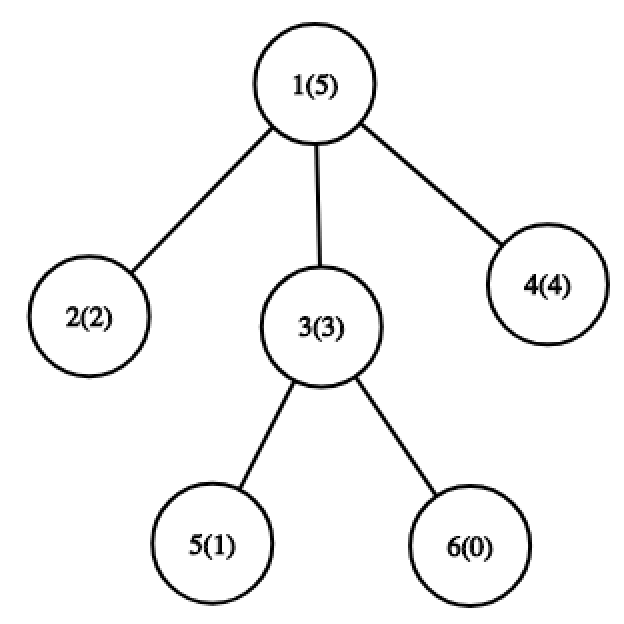
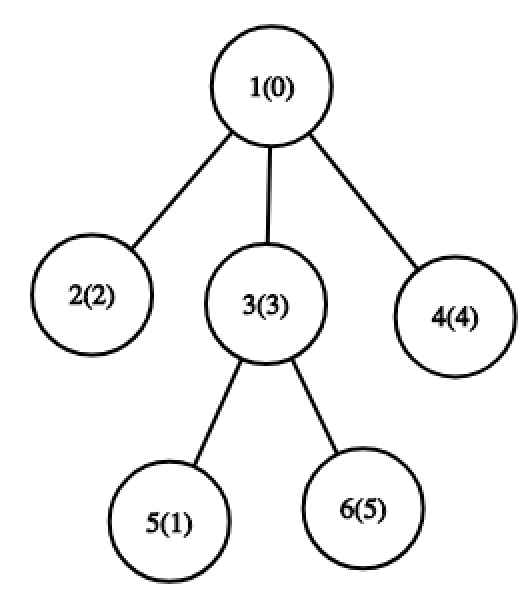
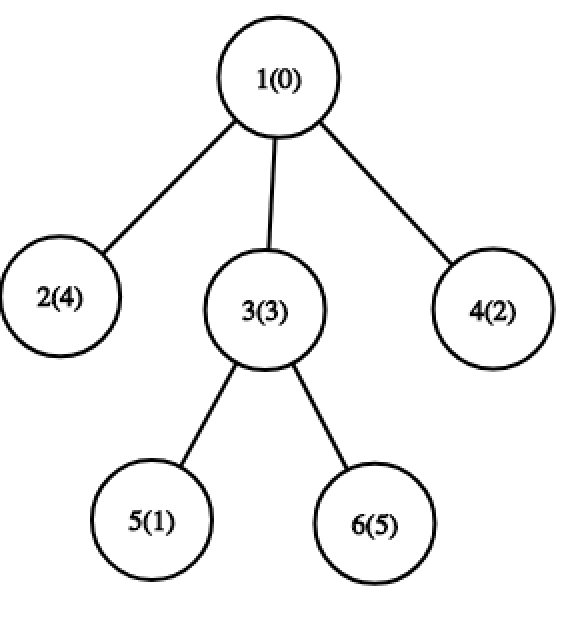
括号中的数字表示节点上的排列值。  在第一个样例中，对于第一个操作，最优路径是从节点 $1$ 到节点 $5$。此时集合为 $\{0, 1, 2\}$，$MEX$ 为 $3$。  对于第三个操作，最优路径是从节点 $5$ 到节点 $6$。此时集合为 $\{0, 1, 4\}$，$MEX$ 为 $2$。  在第二个样例中，对于第一个操作，最优路径是从节点 $2$ 到节点 $6$。此时集合为 $\{0, 1, 2, 5\}$，$MEX$ 为 $3$。  对于第三个操作，最优路径是从节点 $5$ 到节点 $6$。此时集合为 $\{0, 1, 3\}$，$MEX$ 为 $2$。  对于第五个操作，最优路径是从节点 $5$ 到节点 $2$。此时集合为 $\{0, 1, 2, 3\}$，$MEX$ 为 $4$。  对于第七个操作，最优路径是从节点 $5$ 到节点 $4$。此时集合为 $\{0, 1, 2, 3\}$，$MEX$ 为 $4$。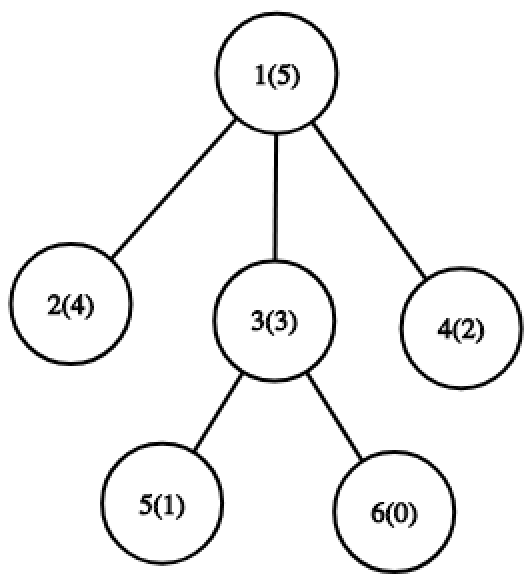  对于第九个操作，最优路径是从节点 $6$ 到节点 $5$。此时集合为 $\{0, 1, 3\}$，$MEX$ 为 $2$。 由 ChatGPT 4.1 翻译