CF1085C Connect Three

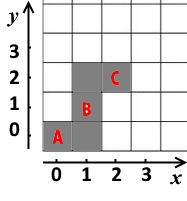
Squareland 国家森林被划分为等大的 $1 \times 1$ 正方形地块，这些地块按照南北和东西方向排列。每一块地可以通过其西南角的整数笛卡尔坐标 $(x, y)$ 唯一确定。 三位朋友 Alice、Bob 和 Charlie 打算在森林中购买三块不同的地 $A, B, C$。最初，森林中的所有地块（包括 $A, B, C$）都被树木覆盖。朋友们希望能够相互拜访，因此他们需要清理一些地块上的树木。清理后，应该能够从 $A, B, C$ 中的任意一块地出发，通过相邻的已清理地块到达其他任意一块地。两块地相邻当且仅当它们有一条边相连。 例如，$A=(0,0)$，$B=(1,1)$，$C=(2,2)$。最少需要清理 $5$ 块地。下图中用灰色表示其中一种清理方式。  当然，朋友们不想太辛苦。请你帮他们计算出最少需要清理多少块地。

第一行包含两个整数 $x_A$ 和 $y_A$，表示地块 $A$ 的坐标（$0 \leq x_A, y_A \leq 1000$）。接下来的两行分别以相同格式给出地块 $B$ 和 $C$ 的坐标 $(x_B, y_B)$ 和 $(x_C, y_C)$（$0 \leq x_B, y_B, x_C, y_C \leq 1000$）。保证三块地的坐标互不相同。

第一行输出一个整数 $k$，表示最少需要清理的地块数。接下来的 $k$ 行，每行输出一块需要清理的地块的坐标。所有 $k$ 块地的坐标应互不相同，输出顺序不限。 如果有多种方案，输出任意一种均可。

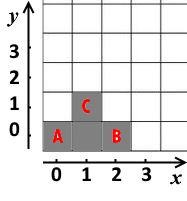
第一个样例如题目描述中的图片所示。 第二个样例如下图所示：  由 ChatGPT 4.1 翻译